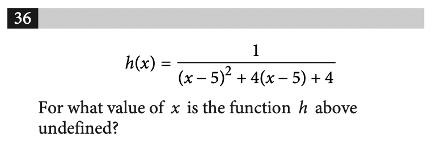The Ultimate Guide to the SAT Math Grid-In Questions
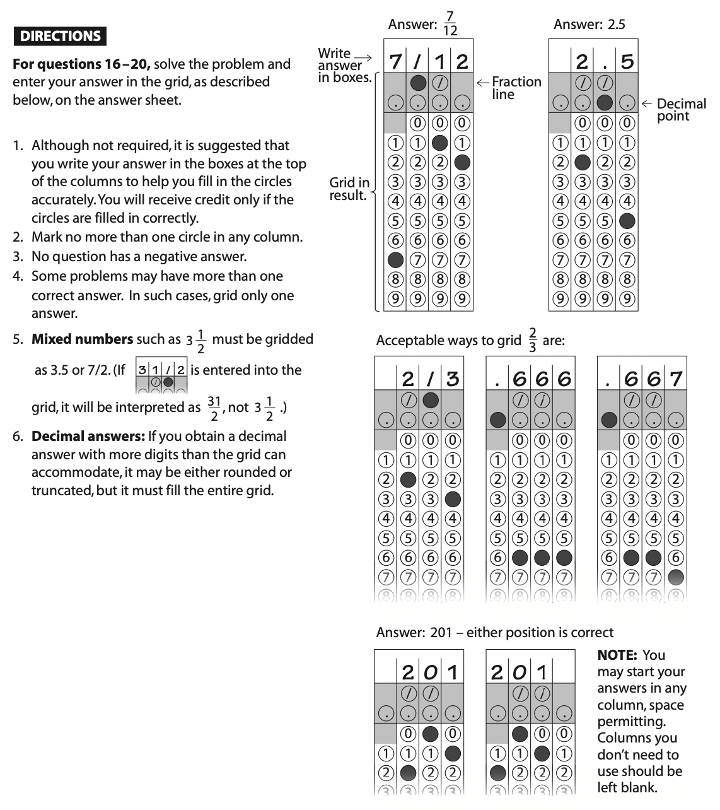
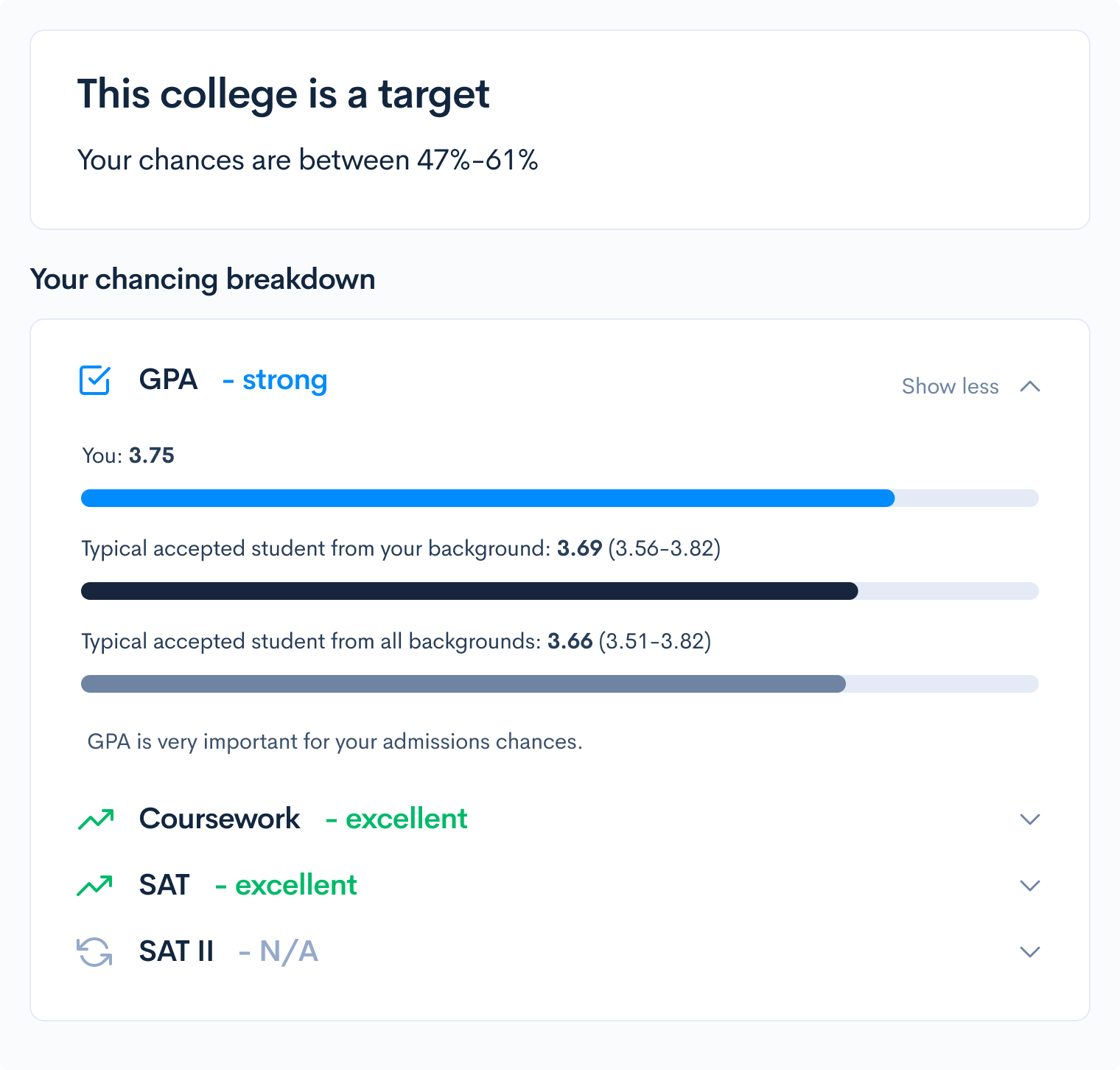
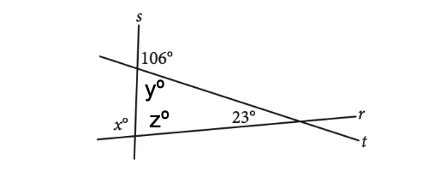
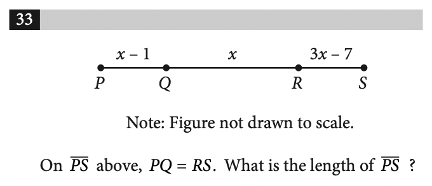
If you’re unsure of the answer for a multiple-choice question, you can always resort to the process of elimination or guess and check. With grid-in questions, however, it’s not as easy. In this post, we’ll discuss strategies for how to approach these problems on the SAT math test, along with sample questions and explanations. The SAT Math Test is composed of two sections: 1. No calculator (25 minutes) 2. Calculator (55 minutes) As you can see, grid-in questions constitute about 22% of the total questions on the SAT Math Test. These questions appear at the end of each section, but recall that you’re allowed to flip back and forth within each section. The SAT Math Test provides the following instructions before grid-in questions: It’s better to have these directions memorized to save you the time of reading and understanding them during the actual SAT test. Many colleges use a metric called the Academic Index (AI) to assess an applicant’s strength. Your AI is calculated based on statistics like GPA or test scores. Some selective schools even automatically reject applicants if their AIs are too low– though this has changed recently due to COVID-19. To see how your SAT score compares to other applicants, take a look at CollegeVine’s free Admissions Calculator. This tool will assess your chances at the colleges of your choice, give you tips on how to improve your profile, and, best of all, is completely free! Keep the following strategies in mind as you attempt SAT math grid-in questions. Like most other questions on the SAT, grid-in questions are designed to trick you. Careful reading is an excellent strategy to avoid being tricked. As you take practice tests, try actively reading math questions. This involves circling or underlining important information, minimizing the chances of making careless mistakes. Unlike multiple-choice questions, grid-in questions don’t have the added benefit of answer choices available to you. This means that if you make a calculation error on a multiple-choice question, you’ll be more likely to catch that error (if your answer isn’t one of the options). So, checking your work is especially important with grid-in questions. If you have the time, go back and double check your calculations to ensure that a minor arithmetic error isn’t the reason you miss easy points. For the grid-in questions on the SAT Math Calculator section, becoming familiar with your calculator is especially important. This will not only help you get the right answer, but it will save you time if you’re comfortable with the different functions available to you. As stated earlier, calculation errors are more difficult to catch with grid-in questions, so strong calculator skills are crucial to ensure your best chances of success. As you complete sample problems and take practice exams, make sure to practice with the same calculator that you’ll be using on the actual test. Since each question in a given section of the SAT carries equal weight, it makes more sense to spend time on many easy questions than one particularly difficult question. So, when you reach the grid-in questions, briefly skim them and start with the ones that seem the most easy. Sometimes, the grid-in questions can be fairly complicated, multi-step problems. If you reach a question that you feel like you can figure out, but it will take you a longer amount of time, skip it and come back to it. This way, you’ll maximize the amount of points you accrue on the SAT Math Test. Here are 10 practice grid-in SAT math questions which are on the tougher side. For this question, we can start with what we are given. Since we are told that \(a=5\sqrt{2}\), we can multiply both sides of the equation by \(2\). This yields \(2a=10\sqrt{2}\). Now, we can use the second equation to get that \(10\sqrt{2}=\sqrt{2x}\). We then use algebra to solve for \(x\): \((10\sqrt{2})^2 =(\sqrt{2x})^2\) \(100(2)=2x\) \(x=100.\) Answer: 100 This question is very text-heavy, so active reading would be helpful. Let’s breakdown the important information: The weight limit is \(6000\) pounds. The truck and driver weigh \(4500\) pounds. Each box weighs \(14\) pounds. We want to keep the total weight less than the bridge’s weight limit, so we have that: \(Total Weight \leq 6000\) The total weight includes the truck, driver, and boxes. Also, if we have \(x\) boxes, and the weight of each is \(14\) pounds, the weight of the boxes would be \(14x\). This means that the total weight is \(4500 + 14x\). Then, \(4500+14x\leq 6000.\) \(14x \leq 1500\) \(x\leq 107.14\) Since we can’t have a fraction of a box, and we want to keep the weight under the limit, we round our answer down to \(107\) boxes. Answer: 107 This question may seem complicated since we are given a lot of information, some of which isn’t entirely relevant to solve the problem. The question asks for the number of time slots that can be sold on Tuesday and Wednesday. Since we are given two days, this is a total of \(48\) hours. But, the time slots are given in minutes, so rather than convert \(48\) hours to minutes (which will result in a large number), let’s convert the time slot to hours. A \(30\) minute time slot is \(0.5\) hours, and we are given a window of \(48\) hours. To determine the number of time slots available, let’s divide: \(48/0.5=96\) Answer: 96 [amp-cta id='9353'] For \(h\) to be undefined, we need the denominator equal to \(0\). So, we’re essentially solving: \((x-5)^2 + 4(x-5)+4=0.\) We can solve this question in two different ways. Method 1: Expansion If you’d prefer the straightforward way of solving, we can simplify the given polynomial: \((x-5)^2 + 4(x-5)+4=0\) \((x^2 -10x+25)+(4x-20)+4=0\) \(x^2 -6x+9=0\) \((x-3)^2 =0\) \(x=3.\) This method will guarantee you the right answer, but might be tricky since there are a lot of steps in the process, which means more chances to make mistakes. If you’d prefer to skip some of the algebra, try this alternate method. Method 2: Substitution For this method, let’s substitute: \(a=x-5\). Then, our equation becomes: \(a^2 +4a +4=0\) \((a+2)^2 =0\) \(a=-2.\) From here, we refer to our substitution to solve for \(x\): \(-2=x-5\) \(x=3.\) Answer: 3 We’ll need to set up our own equations to answer this question. Let’s start by defining our variables: Let \(h\) be the number of calories in a hamburger. Let \(f\) be the number of calories in an order of fries. From the first sentence, we get the following equation: \(h=f+50\). From the second sentence, we get the following equation: \(2h+3f=1700.\) Since we have two equations and two unknowns, we can solve for each variable. Let’s substitute the first equation into the second: \(2(f+50) +3f=1700\) \(2f+100+3f=1700\) \(5f=1600\) \(f=320\) So, from our first equation, \(h=(320)+50=370\). Answer: 370 This type of question often appears on the SAT Math Test. Since we are given that the first 10 ratings have an average of \(75\), we know the total of all 10 ratings is \(10(75)=750.\) Since the store wants an average of at least \(85\) for the first 20 ratings, we must have the total of the first 20 ratings to be greater than or equal to \(20(85)=1700.\) This next part is a little tricky. If we want the lowest possible value for the 11th rating, we have to assume that the 12th to 20th ratings are as high as possible (because the higher those ratings are, the lower the 11th rating can be to still maintain the average we want). So, let’s assume that those remaining 9 ratings are each \(100\) (which is the highest possible value). Then, the total of the remaining 9 ratings is \(9(100)=900\). Let \(x\) represent the 11th rating, so we get: (First 10 ratings) + \(x\) + (Last 9 ratings) \(\geq 1700\) \(750+x+900\geq 1700\) \(x\geq 50.\) Answer: 50 Though we are given inequalities, we can solve this like a system of equations. Let’s use the process of elimination. This requires us to multiply the second equation by \(3\), so we get: \(3y\leq 15x\) Then, we add the two equations: \(y\leq -15x + 3000\) \(3y\leq 15x\) \(4y\leq 3000\) \(y\leq 750.\) Answer: 750 We are given the formula \(N=rT\), where \(N\) is the average number of shoppers in the store at any given time, \(r\) is the rate of shoppers per minute, and \(T\) is the average number of minutes a shopper stays in the store. The question gives us that \(84\) shoppers per hour make a purchase, and each of them spends an average of \(5\) minutes in line. Essentially, we are given \(r\) and \(T\) and are told to find \(N\). This question is difficult because you may be tempted to multiply \(84\) and \(5\). But, we are not given values with the correct units. We are told there are \(84\) shoppers per hour, but we need to know how many shoppers there are per minute. We can set up the following conversion: \(\frac{84 shoppers}{1 hour} \cdot \frac{1 hour}{60 minutes}=1.4 shoppers/min\) Now, we can multiply: \(N=rT=1.4(5)=7.\) Answer: 7 This question relies on triangle knowledge. We can start by marking the unknown angles: Since the two angles form a line, we have that \(106º + yº = 180º\). We can solve for \(y\) and get that \(y=74\). Next, we can consider the angles which form a triangle. The three angles of a triangle should add up to \(180º\), so we have the following equation: \(23º + yº + zº = 180º\) \(23º + 74º + zº = 180º\) \(z = 83.\) For our last step, notice that angles \(x\) and \(z\) also form a line: \(xº + zº = 180º\) \(xº + 83º = 180º\) \(x = 97.\) Answer: 97 Though this question involves geometry, it’s really testing your algebra skills. Since \(PQ=RS\), we know that \(x-1=3x-7.\) We can simplify to solve for \(x\): \(-2x=-6\) \(x=3.\) We know that \(PS\) is the sum of each line segment, so we have: \(PS=(x-1)+x+(3x-7)=3-1+3+3(3)-7=7.\) Answer: 7 Here are some additional resources to guide you as you prepare for the SAT Math Test: 
What’s Covered:
Overview of the SAT Math Grid-In Questions
How Will the SAT Impact My College Chances?
Strategies for Grid-In Questions
1. Read carefully
2. Check your work
3. Know your calculator
4. Start with easier or shorter problems
10 Difficult Grid-In Math Questions
Question 1
Question 2
Question 3
Question 4
Question 5
Question 6
Question 7
Question 8
Question 9
Question 10
Additional Resources