30 SAT Math Formulas You Need to Know
Have you ever been stumped on a math test question, only to realize how simple it was when you later reviewed your test? That’s exactly what happens to many students who take the SAT.
The SAT covers a wide range of math—from as early as elementary school all the way to senior year of high school. While you probably learned these formulas at some point, it may have been a while since you’ve had to use them. This is part of what makes the SAT challenging: since it draws on many different types of math, you need to get out of the high school math mindset (where you only remember what you’ve learned the last month or so to ace the test) and review the math you’ve learned over the years.
If you don’t do any studying for the SAT, you’ll take longer to recall certain helpful formulas and concepts. While there’s always more than one way to reach the right answer, being able to quickly remember these math facts will help you answer questions more efficiently and minimize careless mistakes. We’ve categorized these formulas to help you focus your preparation, and we’ve provided a quick review of what each concept is.
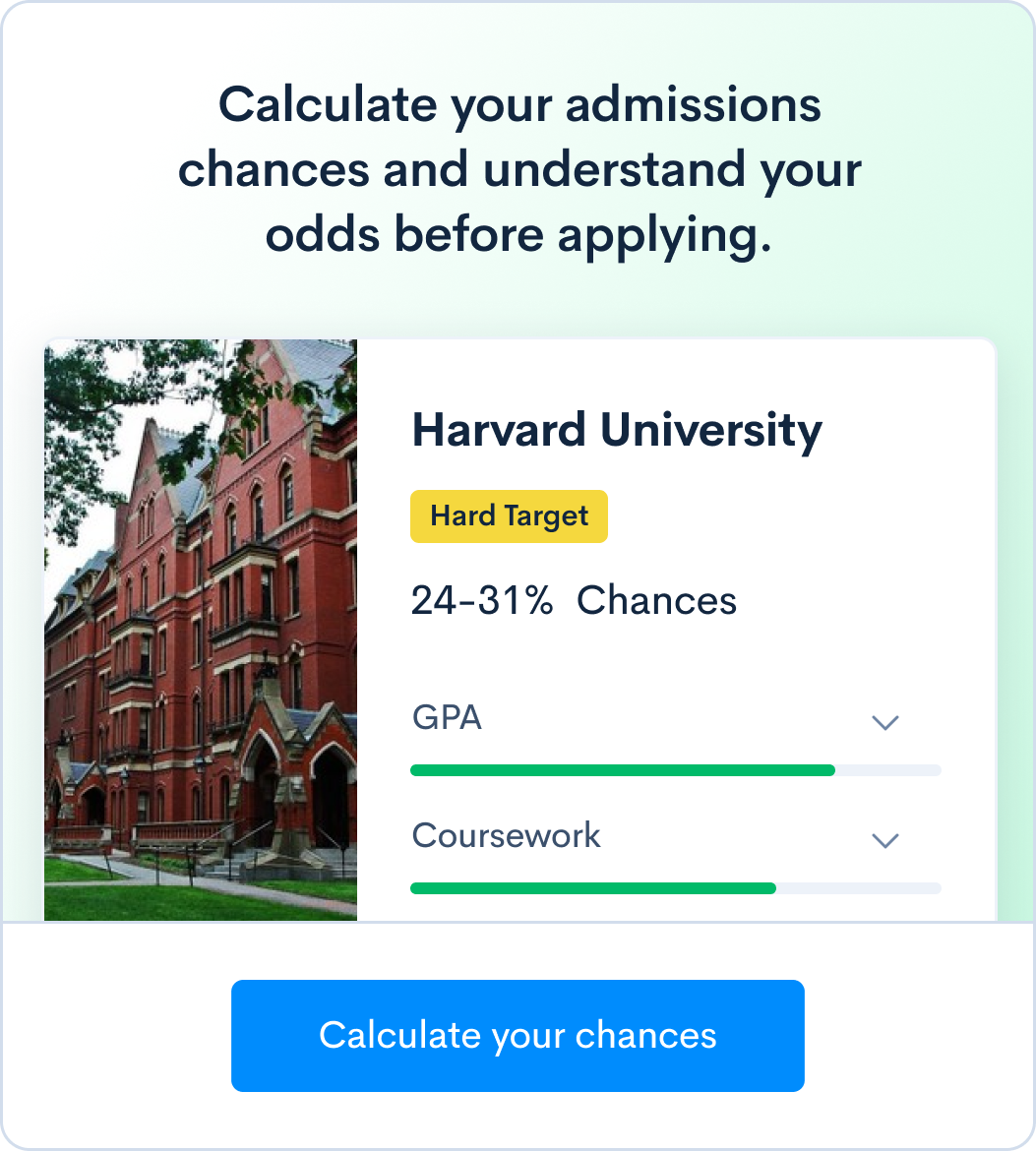
Want to know your chances at the schools you’re applying for based on your SAT score? Calculate your admissions chances right now.
Also, check out our video on how to ace the SAT math section!
Arithmetic and Algebra
1. Slope-Intercept Form of a Line
\(y=mx+b\)
The \(m\) in the equation represents the slope of the equation, and the \(b\) represents the y-value of the y-intercept. For example, if we have the equation \(y=2x+4\), then the slope is \(2\) and the y-intercept is \((0,4)\).
2. Vertex Form of a Parabola/Quadratic
\(y=a(x-h)^2+k\)
You may be more familiar with a quadratic in its factored form, or in the form \(y=ax^2+bx+c\). However, you should be able to recognize vertex form and convert quadratics to this form for the SAT. The values of \(h\) and \(k\) give you the coordinates of the vertex, \((h,k)\).
3. Distance Formula
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
The distance formula is derived from the Pythagorean Theorem (covered later in this post) and it’s useful for quickly finding the distance between two points. Take the values of the coordinates and plug them into this formula to find the distance, and be sure to apply the squares and the square root at the right step.
4. Quadratic Formula
\(x=\frac{-b\:\pm\:\sqrt{b^2-4ac}}{2a}\)
The quadratic formula helps you find the roots of a quadratic equation (parabola) if you can’t easily factor it. You need the quadratic to be in the form \(y=ax^2+bx+c\), and then you simply plug the coefficients and constants into the formula. Note that you will get two answers because there is the plus and minus sign in the numerator.
5. Exponent Rule (Multiplication)
\(a^na^m=a^{n+m}\)
Knowing how to manipulate exponents in a variety of ways will help you tremendously on the SAT, especially the no-calculator portion. In this case, if you have the same base number raised to different powers being multiplied together, you can add the exponents together.
6. Exponent Rule (Division)
\(\frac{a^m}{a^n}=a^{m-n}\)
Similar to the multiplication rule above, if you have the same base number raised to different powers being divided, you can subtract the exponents. You can also rewrite the expression on the right to mirror the one on the left.
7. Exponent Rule (Power Raised to a Power)
\((a^n)^m=a^{n\:\cdot\:m}\)
To continue the exponent rules, raising a power to another power is the same as multiplying the exponents together. This is not an exhaustive list of ways to manipulate exponents, so if you find that you don’t remember these at all, be sure to brush up!
8. Binomial Product 1—Difference of Squares
\((x-y)(x+y)=x^2-y^2\)
The best times to recognize the binomial products and quickly factor them is on the no-calculator section. You don’t have to FOIL or use any other method—you can quickly convert from the factored form to the expanded form on sight. The difference of squares is used often by SAT test makers in a variety of contexts.
9. Binomial Product 2—Perfect Squares Trinomial (Positive)
\((x+y)^2=x^2+2xy+y^2\)
Students sometimes forget the perfect squares trinomial once they’ve left their algebra class, but this is also a good one to recognize. It saves you time because you can quickly convert from one form to another, but it’s a little more difficult to catch than the expanded difference of squares. A good way to know if you’re dealing with one is to look at the first and last values—are they perfect squares?
10. Binomial Product 2—Perfect Squares Trinomial (Negative)
\((x-y)^2=x^2-2xy+y^2\)
This is similar to the above trinomial, except that the quantity involves subtraction rather than addition. While the factored form doesn’t include coefficients, the binomial products on the SAT often do. Practice recognizing these patterns by inputting coefficients in front of \(x\) and constants for \(y\) on the left-hand side. Then multiply out the expression to see how the pattern works with different combinations.
11. Complex Conjugate
\((a+bi)(a-bi)=a^2+b^2\)
On most SAT Math tests, there will be at least one question that involves manipulating imaginary numbers. The complex conjugate allows you to get rid of the imaginary part of a complex number and leaves with you a real number (notice how it resembles the difference of squares!). When given a complex number in the form \(a+bi\), the conjugate is \(a-bi\).
12. Exponential Growth and Decay
\(y=a(1\:\pm\:r)^x\)
This is technically two different equations, one where there is a plus in the equation and one where there is a minus. Knowing the general format of exponential equations will help you on several SAT questions, as you may need to interpret or manipulate these equations. The value \(a\) is the initial value, \(r\) is the rate of growth when it’s positive and the rate of decay when it’s negative.
Ratios, Percentages, and Statistics
13. Simple interest
\(A=Prt\)
This one appears less often than compound interest on the SAT, but it still shows up, so it’s worth knowing. \(P\) represents the principal amount, \(r\) is the interest rate expressed as a decimal, and \(t\) is for time, usually in years.
14. Compound interest
\(A = P(1 + \frac{r}{n})^{nt}\)
The good news is that \(P\), \(r\), and \(t\) mean the same thing in this equation as they do in simple interest. The \(n\) represents the number of times that the interest is compounded during \(1\:t\). For example, if the interest is compounded quarterly over the course of a year, then \(n=4\).
15. Average/Mean
In math, the words average and mean are the same thing: the number you get when you take the sum of a set and divide it by the number of values in the set. You could also think of it as the sum divided by the count. You should know how to calculate an average and interpret it. Be sure to understand the difference between mean and median.
16. Random Sampling
This isn’t technically a formula, but many of the statistics-based problems on the SAT focus more on interpreting concepts in context rather than performing mathematical operations. Random sampling is when you select participants for a study at random within your population. It ensures that your study is representative of the population.
17. Random Assignment
Random assignment is when the participants in a study are assigned a treatment or trial at random. It reduces bias in your study, and means that you can attribute causation in regards to the treatment. On the SAT, you’re often asked about what will reduce bias, or how much you can generalize results to the rest of the population. In these instances, you need to identify random sampling and random assignment.
18. Standard deviation
You won’t need to calculate standard deviation for the SAT, but you will be tested on it conceptually, as with with random sampling and random assignment. Standard deviation is the measure of spread in the data set. A higher standard deviation means greater spread, and lower standard deviations mean smaller spread. You’ll need to know how changes in the data set might affect the standard deviation by making it greater or smaller.
Geometry and Trigonometry
19. Area of an Equilateral Triangle
\(A=\frac{\sqrt{3}s^2}{{4}}\)
The regular area of a triangle formula is provided on the SAT reference sheet, but it requires that you know the height of a triangle. Sometimes you aren’t given the height and you’ll need to calculate it, but you can quickly find the area of an equilateral triangle by plugging the length of one of its sides into the formula above. No need to calculate the height!
20. Equation of a Circle
\((x-h)^2+(y-k)^2=r^2\)
There is usually one question involving the equation of a circle. In this equation, \((h,k)\) is the coordinate for the center of the circle, and \(r\) is the radius of the circle.
What role does your SAT score play in getting accepted to your dream school? Find out by calculating your chances now.
21. Sine Ratio
Some students get nervous when they hear that trig is on the SAT, but it most often appears in the form of trig ratios. Remember that for a given angle in a right triangle, the value of sine is the length of the opposite side divided by the length of the hypotenuse, or opposite/hypotenuse.
22. Cosine Ratio
Just like with sine, remember what the cosine ratio is: the length of the adjacent side divided by the length of the hypotenuse, or adjacent/hypotenuse.
23. Tangent Ratio
Last but not least, the tangent ratio is the length of the opposite side divided by the length of the adjacent side, or opposite/adjacent. Some students find the mnemonic SOH CAH TOA helpful for remembering trig ratios.
24. Degrees to Radians
While the most common form of trig are the basic ratios, you may encounter things like the unit circle or more advanced math. If you need to convert degrees to radians, multiply the degrees by \(\frac{\pi}{180}\). If you need to convert radians to degrees, multiply the radians by \(\frac{180}{\pi}\).
25. Pythagorean Theorem
\(a^2+b^2=c^2\)
The Pythagorean Theorem applies to right triangles, and allows you to solve for one of the side lengths given any other side length. \(a\) and \(b\) are the legs of the triangle, and \(c\) is the hypotenuse.
26. Regular Polygon Interior Angle
\(\frac{(n-2)180}{n}\)
The SAT will probably involve one question with a regular polygon that isn’t a triangle or square. Regular polygons have unique and consistent properties based on their number of sides, and knowing these properties can help you solve these problems. This equation tells you what the degree measure at each angle is based on the number of sides \(n\).
27. 3-4-5 triangle
The SAT provides you with two special right triangles you may already be familiar with on your reference sheet—the 30-60-90 and 45-45-90 triangles. However, the 3-4-5 is a special right triangle with sides that are straightforward integers. This triangle is often incorporated into SAT problems, especially the no-calculator portion, so be on the lookout for it! It can save you having to use the Pythagorean theorem.
28. 5-12-13 triangle
Another special right triangle with whole-number sides, the 5-12-13 triangle is less well-known and shows up less often than 3-4-5. Still, it helps to be able to quickly solve the remaining sides without the Pythagorean theorem, so check for these numbers or their multiples in triangle problems.
29. Length of Arc in a Circle
\(length\:of\:arc = \frac{central\:angle}{360}\pi d\)
Although geometry questions don’t make up a huge portion of the SAT, you may still find a question either about arcs or sectors in a circle. An arc is the length between two points on a circle, usually measured by extending two radii from the center of the circle with an angle formed between them. You can use the degree measure of the arc as a fraction of \(360\) and multiply it by the equation for the circumference to find the length of the arc.
30. Area of Sector in a Circle
\(area\:of\:sector=\frac{central\:angle}{360}\pi r^2\)
Like an arc, the sector is the area in between two radii extending from the circle, sort of like a slice of pie. Again, multiply the degree measure as a fraction of \(360\) and multiply it by the equation for the area of a circle to find the area of the sector.
Wrapping it Up
Before you go, we’re going to offer you a bonus tip: you may want to memorize the perfect squares and perfect cubes. This can help you with quadratic equations that often involve squares, and cubes are often used in solving problems with exponents. Memorizing these will cut down on your need to do math with scratch paper or calculator.
The best way to be able to remember formulas is to practice using them. Unlike your high school math test, where you know what topics will be covered, the SAT will simply present you with a question—it’s up to you to determine what formulas apply. When you practice using formulas with a variety of problems, you’ll be able to quickly identify which formula to use.
Preparing for the SAT? Download our free guide with our top 8 tips for mastering the SAT.
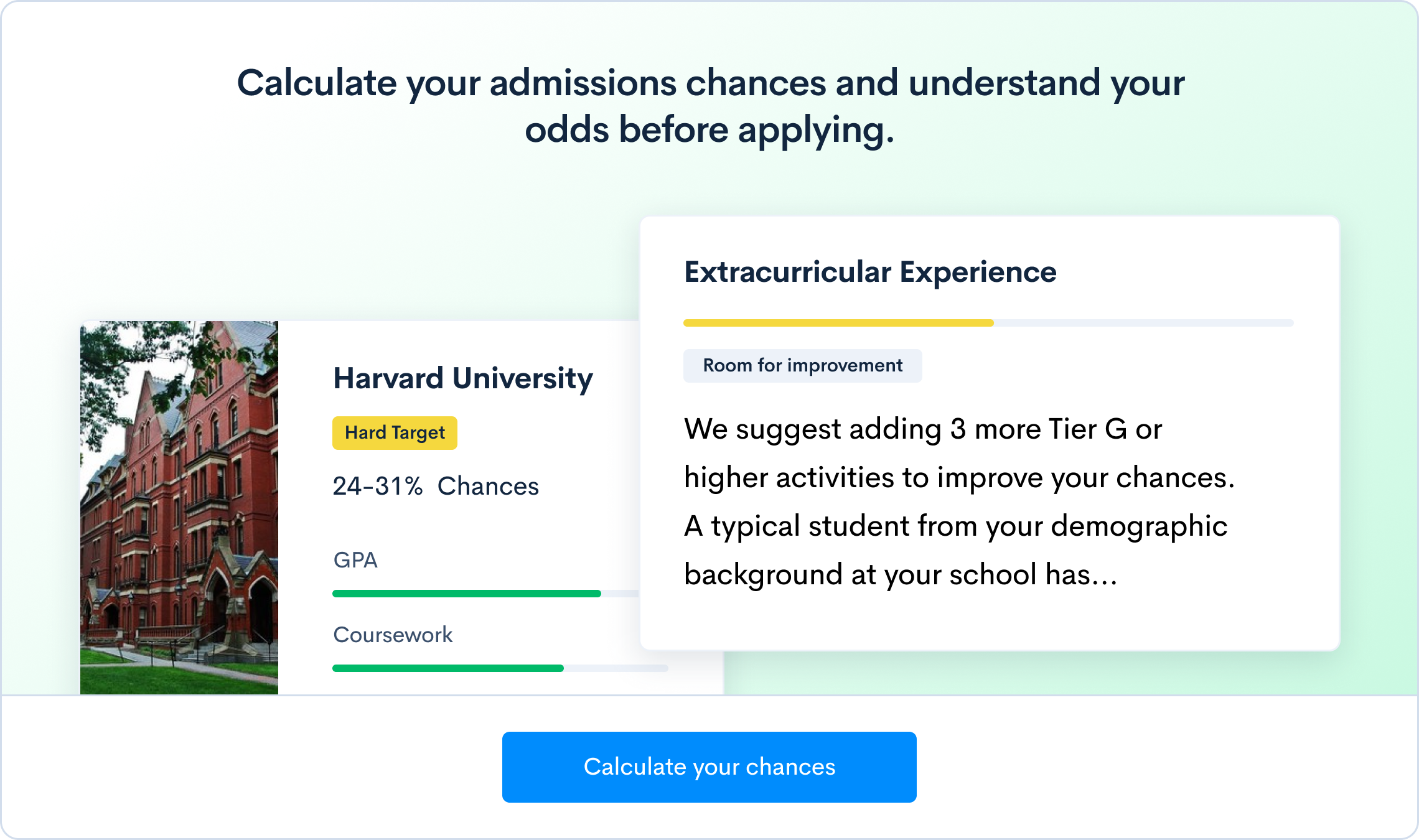
Want to know how your SAT score impacts your chances of acceptance to your dream schools? Our free Chancing Engine will not only help you predict your odds, but also let you know how you stack up against other applicants, and which aspects of your profile to improve. Sign up for your free CollegeVine account today to gain access to our Chancing Engine and get a jumpstart on your college strategy!
Check out some of our other posts on math prep: