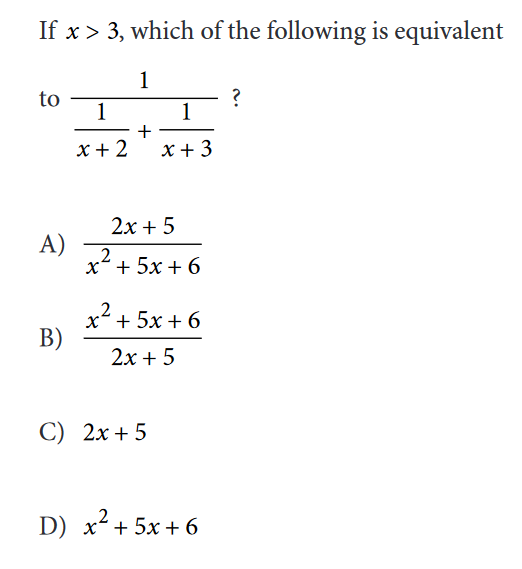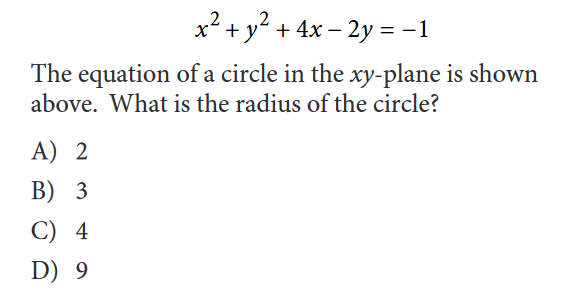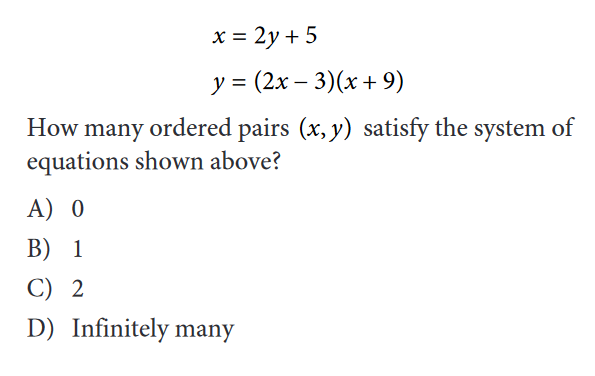15 Hardest SAT Math Questions
Students often want to prepare for the toughest questions they’ll see on the SAT so they can feel confident on test day. We’ve rounded up some of the hardest questions and we’re going to show you how to solve them. These questions come from the free SAT practice tests because we wanted to make sure that we show you questions representative of those you’ll see on the real test. We’ve chosen a variety of question types, but this isn’t an exhaustive representation of all the math topics or types of questions on the SAT. “Hard” is a little subjective; we think these questions are difficult based on working with many students, but you may find some of them easy. In general, you can expect to find harder questions in the second half of each SAT math section, as the questions generally increase in difficulty. For each question below, we’ve identified the key concepts being tested and whether a calculator is allowed. We suggest you try solving these on your own before looking at the answer and our suggested solution. Remember: we’ve given you just one way to solve the problem. Most problems can be solved in a variety of ways! Want to know your chances at the schools you’re applying for based on your SAT? Calculate your admissions chances right now and understand your odds before applying. Before we go into the questions, we want you to understand the terms that the College Board uses to categorize the topics. We’ve also included how many questions fall under each category, so if you’re self-studying, you can prioritize the types of questions that appear more often. Linear equations and inequalities and their graphs and systems. Ratios, proportions, percentages, and units; analyzing graphical data, probabilities, and statistics. Identifying and creating equivalent expressions; quadratic and nonlinear equations/functions and their graphs. This is the only category without a corresponding subscore, but it has a wide variety of topics, including geometry, trigonometry, radians and the unit circle, and complex numbers. A grid-in question can test any of the topics above and is found at the end of each portion of the math test, both no-calculator and calculator. Most students find grid-in questions harder than the multiple-choice because some test tactics—like substituting answer choices into the problem—don’t work. You’ll need to find the correct solution without any help from answer choices. If you develop your math skills, however, then these questions won’t be that much more difficult for you. Now grab a calculator, a pencil and a piece of paper, and let’s review the hardest SAT math questions! Answer: 750 Category: Heart of Algebra—systems of linear inequalities Here’s how to solve it: Answer: C Category: Problem-solving and data analysis—analyzing graphical data, probability Here’s how to solve it: Answer: A Category: Passport to Advanced Math—exponents Here’s how to solve it: Answer: B Category: Passport to Advanced Math—rational equations Here’s how to solve it: \(\frac{1}{\frac{2x+5}{(x+2)(x+3)}}=1\:\cdot\:\frac{(x+2)(x+3)}{2x+5}=\frac{(x+2)(x+3)}{2x+5}\) Note: This is a two-part question, but we left out the first part to focus on the second one. The first question asked for the value of \(x\) in the expression. Because her bank account earns \(2\%\) interest compounded annually, we can convert \(2\%\) to a decimal, giving us \(.02\). We then add \(1\) to this so that we don’t lose the initial deposit. The answer is \(x=1.02\), which you need to know to solve the question above. Answer: 6.11 Category: Passport to Advanced Math—exponential functions and equations (interest) Here’s how you solve it: Is your SAT score enough to get accepted to your dream school? Find out with CollegeVine’s free chancing calculator. Answer: C Additional Topics in Math—complex numbers Here’s how you solve it: \(\frac{3-5i}{8+2i}\cdot\frac{8-2i}{8-2i}=\frac{(3-5i)(8-2i)}{(8+2i)(8-2i)}\) \((3-5i)(8-2i)=24-6i-40i+10i^2=24-46i-10=14-46i\). \(\frac{14-46i}{68}=\frac{14}{68}-\frac{46i}{68}=\frac{7}{34}-\frac{23i}{34}\) Answer: A Category: Additional Topics in Math—Circles and their equations Here’s how you solve it: \(x^2+4x+y^2-2y=-1\) \((x+2)^2-4+(y-1)^2-1= -1\) \((x+2)^2+(y-1)^2=-1+1+4\) \((x+2)^2+(y-1)^2=4\) [amp-cta id='9353']
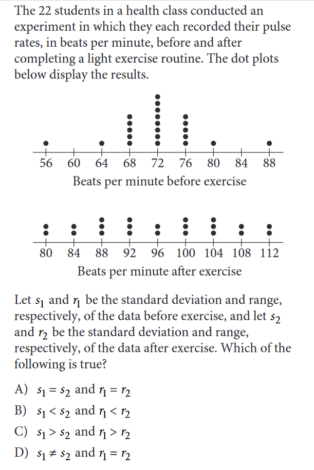
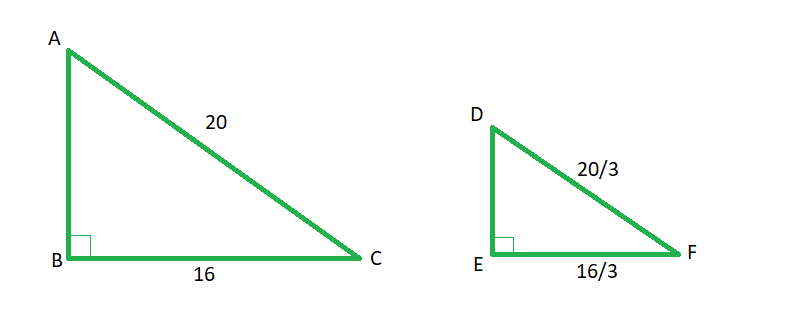
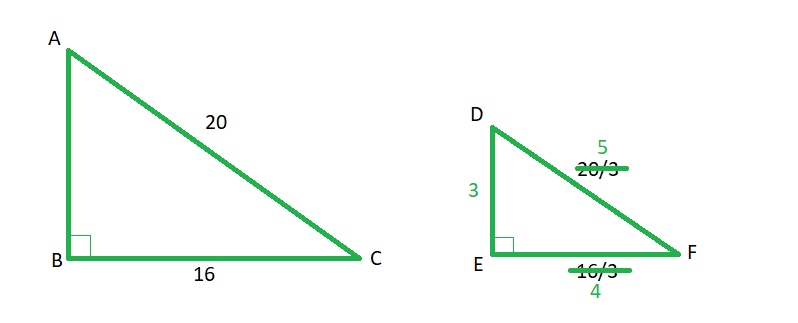
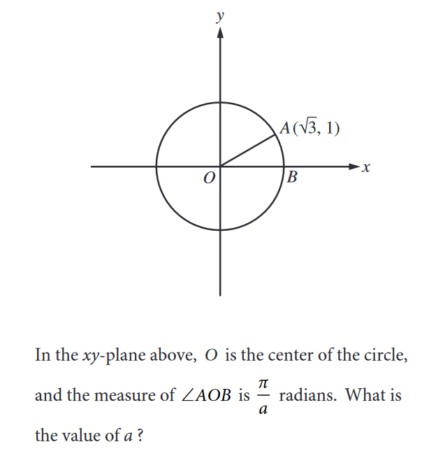
Answer: B Category: Passport to Advanced Math—rewriting equations in terms of another variable Here’s how you solve it: 1. Students get intimidated by questions that have only variables. Remember to use what you know about manipulating equations—such as whatever you do to one side you must do to the other—to handle these problems. 2. We want to rewrite the equation in terms of \(F\). To start, we’ll want to get rid of the \(F\) in the denominator of the equation above by multiplying both sides by \(N+F\) like so: \(R(N+F)=\frac{F(N+F)}{(N+F)}\) \(R(N+F)=F\) 3. Distribute the \(R\) on the left-hand side, and then move all the F‘s to the same side. \(RN+RF=F\) \(F-RF=RN\) 4. Next, we can factor out the \(F\) on the left-hand side and divide both sides by the remaining factor to isolate \(F\) and get our answer. \(F(1-R)=RN\) \(F=\frac{RN}{1-R}\) Answer: D Category: Problem Solving and Data Analysis—standard deviation, range, analyzing graphical data Here’s how you solve it: 1. You won’t have to calculate standard deviation on the SAT, but you will need to know what it means and what affects it. Standard deviation is a measure of spread in a data set, specifically how far the points in the data set are from the mean value. A larger standard deviation means that the points in the data set are more spread out from the mean value, and a smaller one means that the points in the data set are close to the mean value. Likewise, you’ll need to know what is meant by range. Range refers to the difference between the highest and lowest values in a data set. The SAT may require you to calculate the range for a data set. 2. Let’s first determine the standard deviations of each data set relative to each other. In the first data set, most of the data points are clustered around each other, which makes it likely that the mean is somewhere around \(72\) (even though there are two outliers, they are equidistant from \(72\) so they will balance each other out when determining the mean). In contrast, the second data set is more spread out, so we can conclude that the standard deviation of the first set is smaller than the standard deviation of the second. We can eliminate choices A and C. 3. Now let’s look at the range for each set. We can subtract the highest and lowest values for each set to find the range. For the first set, \(88-56 = 32\). For the second set, \(112-80 = 32\). The ranges of each set are equivalent. This leaves us with choice D as our answer. Answer: C Category: Passport to Advanced Math—quadratic and algebraic functions and their graphs Here’s how you solve it: 1. We can solve this using substitution. Substitute the second equation into the first and expand the quadratic: \(x=2[(2x-3)(x+9)]+5\) \(x=2(2x^2+15x-27)+5\) \(x=4x^2+30x-49\) 2. Next, move the x from the left-hand side over to the right. The roots of this quadratic will give us the solution to the system of equations above. \(0=4x^2+29x-49\) 3. Since the roots of the above quadratic will give us the solution to the system of equations above, we can use the discriminant of the quadratic formula to find out how many solutions there are. The discriminant is the part of the quadratic formula under the radical, or \(b^2-4ac\). If the discriminant is positive, there are 2 solutions; if the discriminant is 0, there is 1 real solution (or a repeated solution); if the discriminant is negative, there are no real solutions. Substituting the numbers from the equation into the discriminant formula gives us \(29^2-4(4)(49)=841-784=57\). This is a positive number, which means there are 2 solutions to the system of equations. How do your SAT and SAT Subject test scores influence your chances of admission? Calculate your chances with CollegeVine’s free admissions calculator. Answer: 2.25 or 9/4 Category: Passport to Advanced Math—determining effect of one variable on another Here’s how you solve it: 1. This is similar to the earlier problem where there are only variables, but if we proceed step-by-step and manipulate the equation carefully, we can find the solution. In this problem, we have two fluids, and one of them is moving at a velocity of \(1\) and the other at \(1.5\). We can substitute the \(1.5\) into the equation to see how it might affect \(q\), or the dynamic pressure. \(q=\frac{1}{2}n(1.5v)^2\) 2. Using exponent rules (from Question 3 above) we can rewrite \((1.5v)^2=1.5^2v^2\). Squaring \(1.5\) gives us \(2.25\). 3. For our fluid moving at a velocity of \(1.5\), we thus have: \(q=\frac{1}{2}n(2.25)v^2\). For our fluid moving at a velocity of \(1\), we have \(q=\frac{1}{2}n(1)v^2\). We can thus see that the dynamic pressure of the faster fluid will be \(2.25\) times that of the slower fluid. Answer: 3/5 or .6 Category: Additional Topics in Math—trigonometry Here’s how you solve it: 1. If you’re given a word problem that involves geometry or trigonometry and no diagram, you should draw yourself a diagram and label the information. This often makes it very clear how to find the answer. Here’s our diagram: 2. Many students know about the 30-60-90 and the 45-45-90 right triangles, and information about these triangles is included on the first page of each SAT math portion. However, you should also be on the lookout for the 3-4-5 and 5-12-13 right triangles. College Board likes to use these triangles and their similar counterparts because they have nice, whole-number sides that make calculations easy. Knowing this, we can see that Triangle ABC is similar to the 3-4-5 triangle, each side of ABC 4 times the length of the 3-4-5 triangle. 3. Knowing that triangle ABC is similar to a 3-4-5 triangle, and that triangle DEF is also similar to a 3-4-5 triangle, we can find \(sin\:F\) by substituting 3-4-5 for the sides of DEF and using the definition of sine: \(sin\:\theta\:=\frac{opposite}{hypotenuse}\) 4. With respect to \(F\), the opposite side is \(3\) and the hypotenuse is \(5\). This means that \(sin\:F=\frac{3}{5}\), or \(0.6\). Answer: C Category: Heart of Algebra—linear equations and inequalities in context Here’s how you solve it: 1. You’ll need to be able to write equations that reflect the context described in a word problem for several questions on the SAT, both linear context and non-linear contexts. If you have trouble “translating” word problems into math, this is a skill you’ll want to work on! Rewriting word problems to include words like equal to, less than, more than, sum, and so on can help you easily translate the problem into equations and inequalities. 2. We’re told that Roberto wanted to sell \(57\) insurance policies but he didn’t meet his goal, which means that he sold less than \(57\) insurance policies. Given that \(x\) represents the number of \(\$50,000\) policies sold and \(y\) represents the number of \(\$100,000\) policies sold, the sum of these two numbers is less than \(57\). This is represented as \(x+y\:\lt\:57\). We can eliminate choices B and D. 3. Next, we’re told that the value of all the policies sold was more than \(\$3,000,000\). We need to multiply the value of the policy by the number of that type of policy, which gives us \(50,000x+100,000y\:\gt\:3,000,000\). Choice C is the only answer that reflects Roberto’s insurance policy sales. Answer: A Category: Problem Solving and Data Analysis—Statistics Here’s how you solve it: 1. These kinds of problems can surprise students because there isn’t any obvious calculation or “math” to do. Instead, you’re being asked to interpret the results based on given information, and you’ll need to know statistics to correctly interpret these types of problems. In this case, you’ll want to draw upon knowledge of population parameters, random sampling, and random assignment: 2. The SAT is very particular when including statistical clues and knowing the definitions of statistics. For example, if random sampling is not mentioned in a problem, then the results cannot be generalized to the entire population. Knowing the above, we can see that random sampling and random assignment are explicitly mentioned in this case. We can reasonably conclude cause and effect to be generalized to the population in question, or that it’s likely that Treatment X will improve the eyesight of people who have poor eyesight. The other choices are either too confident in their conclusion or do not specify the population in question. Answer: 6 Category: Additional Topics in Math—Radians Here’s how you solve it: 1. The point \(A\) is \((3,1)\). We can create a triangle to find the degree measure of \(\angle{AOB}\). When we do this, we can use the information the SAT provides to see that this is a 30-60-90 triangle and that the hypotenuse (or the radius of the circle) is \(2\). 3. Since \(a\) is the denominator, the answer is \(6\). We hope that you have a good sense of the type of questions that you might see on the SAT, but just remember that these questions aren’t a complete representation of the topics you could be tested on. Review the questions above and ask yourself: which ones were the most challenging to you? Which topics do you need to brush up on? Check out our free guide with our top 8 tips for mastering the SAT. Want to know how your SAT score impacts your chances of acceptance to your dream schools? Our free Chancing Engine will not only help you predict your odds, but also let you know how you stack up against other applicants, and which aspects of your profile to improve. Sign up for your free CollegeVine account today to gain access to our Chancing Engine and get a jumpstart on your college strategy! To learn more about how to do well on the SAT, check out these other posts:
Math Topics on the SAT
Heart of Algebra: 33% of test, 19 questions
Problem Solving and Data Analysis: 29% of test, 17 questions
Passport to Advanced Math: 28% of test, 16 questions
Additional Topics in Math: 10% of test, 6 questions total
Grid-in Questions
15 Hardest SAT Math Questions
Question 1: Calculator permitted, grid-in response
Question 2: Calculator permitted, multiple choice
Question 3: Calculator not permitted, multiple choice
Question 4: Calculator not-permitted, multiple choice
Question 5: Calculator permitted, grid-in response (see note)
Question 6: Calculator not-permitted, multiple choice
Question 7: Calculator permitted, multiple choice
Question 8: Calculator not-permitted, multiple choice
Question 9: Calculator permitted, multiple choice
Question 10: Calculator not-permitted, multiple choice
Question 11: Calculator permitted, grid-in response
Question 12: Calculator not-permitted, grid-in response
Question 13: Calculator permitted, multiple choice
Question 14: Calculator permitted, multiple choice
Question 15: Calculator not-permitted, grid-in response
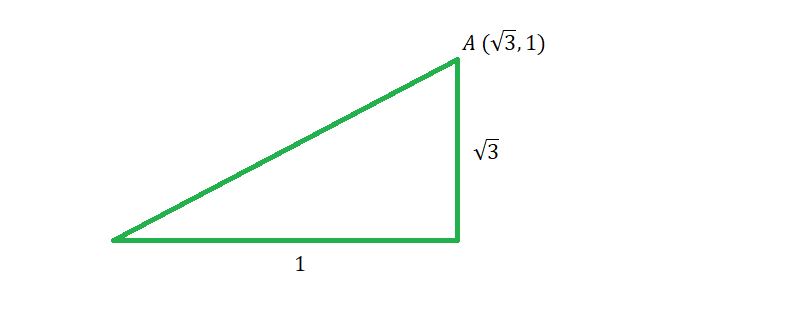 2. This means that \(\angle{AOB}\) is \(30\) degrees. To convert from degrees to radians, we multiply by \(\frac{\pi}{180}\). This is what we get: \(30\:\cdot\:\frac{\pi}{180}=\frac{\pi}{6}\)
2. This means that \(\angle{AOB}\) is \(30\) degrees. To convert from degrees to radians, we multiply by \(\frac{\pi}{180}\). This is what we get: \(30\:\cdot\:\frac{\pi}{180}=\frac{\pi}{6}\)Final Tips