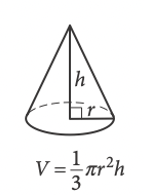Guide to SAT Math Geometry Questions + Practice Problems

What’s Covered:

• Overview of the SAT Math Test
• SAT Geometry Concepts + Practice Questions
• How Will the SAT Impact Your College Chances?

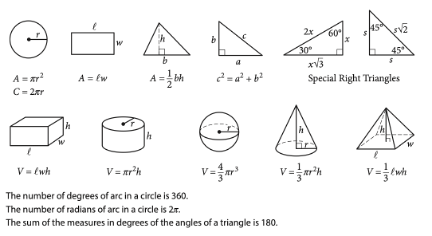
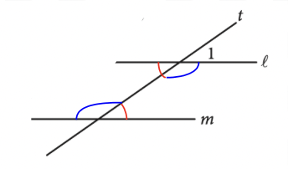
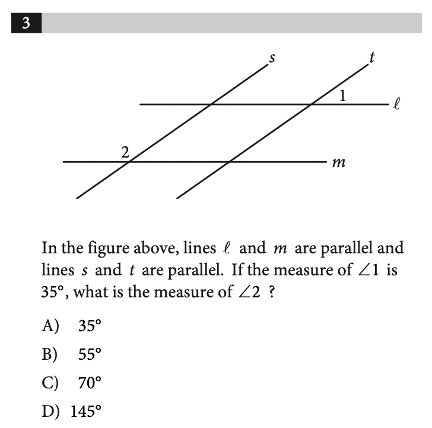
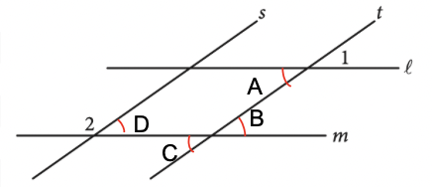
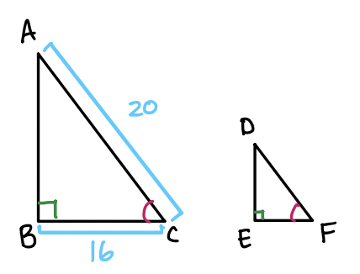
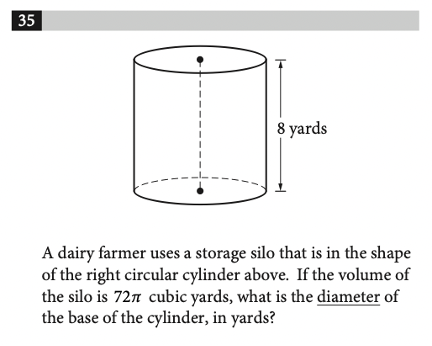
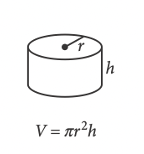
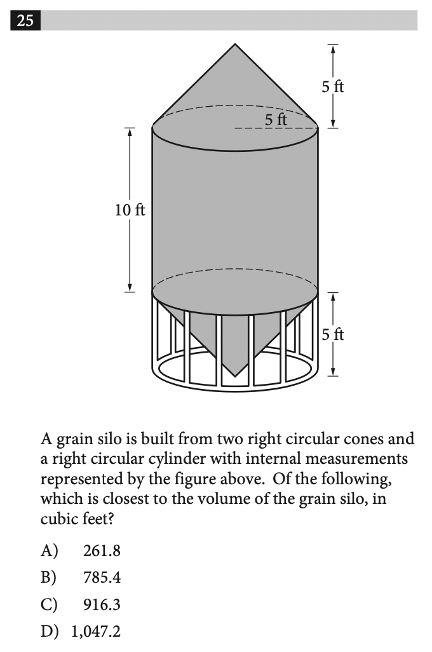
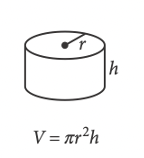
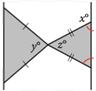
Angles, triangles, solids, and more are bound to show up on the math portion of your SAT Test. So, while studying for the SAT, you should make sure you have a strong foundational knowledge of geometry. Since these problems are often more conceptual than calculation-heavy, knowing basic geometric properties will allow you to quickly answer these types of questions, earning you easy points towards your total score! In this post, we’ll go over some important geometry concepts on the SAT, along with some tough practice problems, so you can test your geometry skills.

Overview of the SAT Math Test

The SAT Math Test consists of two sections: No calculator and Calculator. The No calculator section asks you to answer 20 questions in 25 minutes and the Calculator section asks you to answer 38 questions in 55 minutes. Your scores in both these sections are combined and scaled to be out of 800, or half of your total SAT score.

There are four categories of questions on the SAT Math Test:

1. Heart of Algebra
2. Problem Solving and Data Analysis
3. Passport to Advanced Math
4. Additional Topics in Math

Geometry questions fall under the fourth category, and constitute around 10% of the SAT math test, or around 5–7 questions. The SAT expects you to know basic geometric concepts, like the properties of angles, shapes, and solids. But, you are given a few formulas to help you out with these problems:

However, we recommend having these formulas memorized. This will not only save you the time of flipping back and forth through your test booklet, but will also give you an idea of where to start when encountered with an unfamiliar problem.

Important SAT Geometry Concepts + Practice Questions

Angles

You should definitely expect to be tested on angles on the SAT Math Test. Let’s review angles by going through each of the different types you’ll be expected to know on the SAT.

Acute, right, and obtuse angles

Angles are classified by acute, right, and obtuse according to their angle measure:

• Acute: < 90°
• Right: = 90°
• Obtuse: > 90°

The SAT won’t directly test you on whether an angle is acute, right, or obtuse, but you’re expected to know these terms and will likely encounter them in problems regarding angles.

Vertical angles

 When two straight lines intersect, four angles are formed. The angles which are opposite to each other are called vertical angles, and have equal angle measures.

In this picture, angles A and B are vertical angles. Thus, the measure of angle A is equal to the measure of angle B.

Complementary and Supplementary angles

Complementary angles are two angles which form a right angle and whose measures add up to 90°.

Supplementary angles are two angles which form a straight line and whose measures add up to 180°.

A trick that you should know is that complementary angles have special trigonometric properties:

For any two complementary angles A and B, \(\sin{A} = \cos{B}\) and \(\cos{A} = \sin {B}.\)

Here is an example SAT question which illustrates this property:

Answer: C

Since we have that \(\sin{a°} = \cos{b°}\), you should realize that the two angles are complementary. This means that the angle measures will add up to 90°.

So, \(a+b=(4k-22)+(6k-13)=90.\)

If we simplify, we have that: 

\(10k-35=90\)

\(10k=125\)

\(k=12.5\)

Lines

The first thing you should know about lines is that they contain 180°. This makes sense since earlier we stated that two supplementary angles (angles which together form a line) have an angle sum of 180°.

This characteristic is important when it comes to problems involving parallel lines. A set of parallel lines are lines which will never intersect. Another important term is a transversal, a line which intersects 2 or more parallel lines.

Here is a diagram with a transversal: 

In this diagram, the parallel lines are \(l\) and \(m\). The transversal is line \(t\). A transversal forms alternate interior angles: angles which are inside the two parallel lines and are on opposite sides of the transversal.

In the diagram, the two red angles are a pair of alternate interior angles, and the two blue angles are another pair of alternate interior angles.

Alternate interior angles are special in that they have equal angle measures.

So, in the diagram, the two red angles have the same angle measure, and the two blue angles have the same angle measure.

For practice with transversals, take a look at the following problem:

Answer: D

Since we’re given the measure of angle 1, let’s start by marking up the diagram with all the angles which are equivalent to angle 1:

• Angle A is equivalent to angle 1 since they’re vertical angles.
• Angle B is equivalent to angle A since they’re alternate interior angles. (With \(l\) and \(m\) as the parallel lines and \(t\) as the transversal).
• Angle C is equivalent to angle B since they’re vertical angles.
• Angle D is equivalent to angle C since they’re alternate interior angles. (With \(s\) and \(t\) as the parallel lines and \(m\) as the transversal).

So, all these angles should have measure 35°.

Next, notice that angles 2 and D are supplementary–they form a straight line.

So, their measures should add up to 180°. 

If we consider the measure of angle 2 to be \(x^{\circ}\), we have: \(x^{\circ}+35^{\circ}=180^{\circ}.\)

Then, \(x=145^{\circ}\), and the correct answer is answer choice D. 

Triangles

You’ll definitely need to know about triangles to do well on the SAT Math Test. The following formulas and properties are given to you:

So, the SAT expects you to know how to solve for the area of a triangle, the Pythagorean Theorem, and properties of special triangles. Let’s take a look at some special types of triangles.

Isosceles triangles

Isosceles triangles are triangles with exactly 2 congruent sides. The one, non-congruent side is called the base. To best solve problems regarding isosceles triangles, however, you should also know that the two base angles are congruent.

Here’s an example of an isosceles triangle problem:

Answer: 105

Recall that the base angles of an isosceles triangle are congruent and that the sum of the measures of all the angles in a triangle is 180°.

Let’s start by solving for \(z\) using the equations given.

Substitute \(y=75\) into the equation \(180-z=2y\):

\(180-z=2(75)\)

\(z=30.\)

Now, we can label our diagram to solve for \(x\):

Since the triangle on the right is isosceles, the two red angles should have the same measure, which we can call \(a^{\circ}\).

So, \(z^{\circ}+a^{\circ}+a^{\circ}=180^{\circ}.\)

Since \(z=30, a=75.\)

Then, because angles \(a\) and \(x\) are supplementary, their angle measures should add up to 180°:

\(a°+x°=180°\)

\(75+x=180\)

\(x=105°\)

Similar triangles

You should also be familiar with similar triangles for the SAT Math Test. Similar triangles are triangles that have the same angle measures, but not necessarily the same side lengths. However, we do know that the side lengths are proportional.

To better examine similar triangles, let’s take a look at the following problem:

Answer: 3/5

Let’s start by drawing a diagram with the information given:

Since the two triangles are similar, we have that all the angle measures are equivalent: this is why angles C and F have the same angle measure.

So, \(\sin{F}=\sin{C}\), and we can solve for \(\sin{C}\) to determine the value of \(\sin{F}\).

To find \(\sin{C}\), we’ll need to know the side lengths of the opposite side and the hypotenuse. We already know that the length of the hypotenuse, \(AC\), is 20. 

To find the length of the opposite side, \(AB\), we’ll need to use the Pythagorean Theorem:

\(AB^{2}+BC^{2}=AC^{2}\)

\(AB^{2}+16^{2}=20^{2}\)

\(AB=12\)

So, \(\sin{C}=AB/AC=12/20=3/5.\)

Take a look at some of our other guides to triangles on the SAT:

• 30-60-90 Triangles
• Trigonometry (SOHCAHTOA)

Circles

Circles can be difficult in that there are so many different types of questions that can be asked about them. Check out our in-depth guide to tackling circle problems!

Essentially, you should know the following properties of circles:

• Radius and diameter
• Circumference, area, and volume
• Degrees and radians
• Arcs
• The equation of a circle

Here is a sample problem involving circumference and arcs:

Answer: 1/6

Again, though the formula for circumference is given to you, it’s best to already have it memorized.

Then, you could quickly compute the circumference: \(C=2\pi r=2\pi(1)=2\pi.\)

To find the fraction, divide the length of arc \(\overset{\frown}{AB}\) by the circumference: \(\frac{\pi/3}{2\pi}=1/6\).

Quadrilaterals

Quadrilaterals show up less often on the SAT than triangles and circles, but you should still know their general properties.

A quadrilateral is a polygon that has 4 sides, and common quadrilaterals include squares, rectangles, parallelograms, and trapezoids. 

An important property of quadrilaterals is that the angle measures add up to 360°.

Here is a sample quadrilateral problem:

Answer: D

Since the sum of all angle measures is 360°, we can set up the following equation: \(45^{\circ}+x^{\circ}+x^{\circ}+x^{\circ}=360^{\circ}\)

Let’s simplify to solve for \(x\):

\(45+3x=360\)

\(3x=315\)

\(x=105.\)

Solids

For solids, you’ll likely encounter problems asking you to compute the surface area or volume. Or, they might ask you to use surface area or volume to solve for other properties.

For example, this problem involves using volume to find the diameter of the cylinder:

Answer: 6

This problem requires that you work backwards: given a volume, you must find the diameter of a cylinder. Let’s start by recalling the volume formula for a cylinder:

So, since we know \(V=72\pi\) and \(h=8\), we can easily solve for \(r\):

\(72\pi = \pi r^{2}(8)\)

We isolate \(r\) to get: \(r^{2}=9\).

So, \(r=3\). But, we can’t stop here! The problem asks for the diameter, not the radius, so we must multiply our radius by 2 to get that our diameter is 6 yards.

Here is another problem involving multiple solids:

Answer: D

This problem is straightforward in that you just need to solve for volume, but it can be tricky since it involves multiple solids at once. But, if we find the volume of each solid separately and then just add them together, the problem should be much easier to solve.

Right away, notice that the two right circular cones are identical, so we can just solve for the volume of one and then multiply that value by 2. Let’s recall the volume formulas for cones and cylinders:

From the diagram, we see that the radii for the cones and cylinder are all 5 ft. The height of the cones is 5 ft, and the height of the cylinder is 10 ft.

Let’s first solve for the volume of each cone: \(V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\pi (5)^{2}(5)= 130.9 ft^{3}\)

So, the volume of both the cones is: \(2(130.9)=261.8 ft^{3}\)

Now, let’s find the volume of the cylinder: \(V=\pi r^{2}h=\pi (5)^{2}10=785.4 ft^{3}\)

So, the total volume of the solid is: \(261.8+785.4=1,074.2 ft^{3}\)

How Will My SAT Score Impact My College Chances?

Your SAT score, along with other statistics (like your standardized test scores and GPA) is used to calculate a metric called the Academic Index (AI). Many selective colleges use AI to determine an application’s strength. In fact, some colleges will even automatically reject applicants with too low AIs–though this has changed in some cases due to COVID-19 and test-optional policies.

If you want to see how your SAT score impacts your chances at the schools you’re interested in, check out CollegeVine’s free Admissions Calculator! This tool will not only show you how you stack up against other applicants, but will also give you tips on what aspects of your profile might need improvement.

Other posts you may like:

30 SAT Math Formulas You Need to Know

15 Hardest SAT Math Questions