Guide to SAT Math Heart of Algebra + Practice Questions
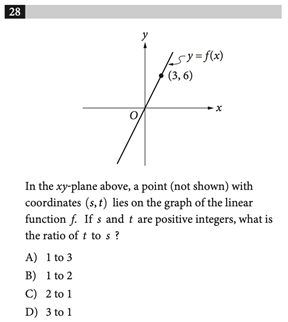
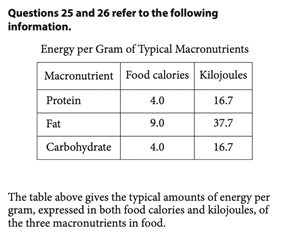
The Heart of Algebra questions make up a third of the SAT Math section. If you’re looking to improve your score or even aiming for a perfect 800, here are some strategies and tough questions to test your skills. The SAT Math section is scored out of 800 and constitutes half of the total SAT score. There are three main categories: Heart of Algebra, Problem Solving and Data Analysis, and Passport to Advanced Math. When you take the SAT, you’ll receive a subscore out of 15 for each of these categories. Here is the breakdown of each section: The remaining 10% falls under Additional Topics in Math, which contains a wide array of topics. The Heart of Algebra section focuses on linear equations, inequalities, graphs, and systems. These questions range from simple calculations to more complex word problems. Heart of Algebra questions require that students: In this post, we will explore general strategies to solving Heart of Algebra Problems and cover some of the more difficult problems that you may encounter on the SAT. Selective colleges often use a metric called the Academic Index (AI) to determine an applicant’s strength. Your AI is calculated based on your GPA and SAT/ACT scores, so having a strong academic profile is key to increasing your chances of admission. In fact, if your AI is too low, a college may reject you automatically. If it’s high enough, your application should at least get read. To assess the impact of your SAT score on your chances, CollegeVine has created a free Admissions Chances Calculator. This tool will let you know how competitive your score is and will even offer tips on how to improve the rest of your profile! Though Heart of Algebra problems appear in many different shapes and forms, the basic strategy to solve them is relatively the same from question to question. In general, when taking the SAT math section, remember to skip problems that seem too difficult or that may take too long to answer. Since all questions are weighted the same, answering many easy questions is more beneficial than answering one difficult question. For Heart of Algebra problems specifically, since they center on linear equations, start by underlining or circling relevant information (i.e. any quantities, variables, or relationships that are defined). Then, make sure you understand what the question is asking. Begin by defining variables, then if an equation is not already given to you, construct as many equations as you can, based on the information given. Once your equations are established, use them to solve for what the question initially asked. After solving each problem, make sure to check back and ensure you actually answered the question, or even double check your calculations if you have the time. Here are some sample Heart of Algebra questions which are on the more difficult side, along with a detailed description of how to solve them. Correct Answer: B For multiple choice problems, looking at the answer choices can be helpful in determining how to solve the problem. For this question, the answer choices show us that the question is looking for a system of inequalities. So, when reading the question, let’s pay close attention to any relationships between quantities. The last sentence of the problem defines variables for us: \(x\) is for junior directors and \(y\) is for senior directors. The first sentence says “at least 10 staff members” should be hired. The term “at least” mathematically translates to “greater than or equal to.” So, we have that the total number of directors (which is the number of junior directors and the number of senior directors) must be greater than or equal to 10: \(x+y\:\geq\:10\). This eliminates choices A and D. To choose between B and C, we can save time by noticing that one difference is whether \(x\:\geq\:3\) or \(x\:\leq\:3\). The problem says, “She must hire at least 3 junior directors.” Like before, this indicates \(x\:\geq\:3\), so the correct answer is B. This question is an example of how you don’t always need to solve the entire problem to determine the correct answer. Correct Answer: C A lot of information is given in this equation, so our first instinct should be to try to relate that information. We know that the initial value of the equipment is $32,400 and that every year it depreciates some (unknown) amount. We are also given that at 12 years, the value is $0. If we were to relate value with time, we’d have that \(V=32,400-kt\), where \(V\) represents value in dollars, \(t\) represents time after the purchase in years, and \(k\) represents the unknown amount it depreciates each year. We know this equation should be linear since the question states that the equipment depreciates at a “constant rate.” The reason why we subtract \(kt\) is because the value decreases each year. We also have 32,400 in the equation since, when \(t=0\), we should have that \(V=32,400\) (since at the time of purchase, the value was $32,400). Now, we can use more information to determine \(k\) and complete our equation. We have that when \(t=12, V=0\). Substituting this into our equation, we get: \(0=32,400-k(12)\). When we solve for \(k\), we have that \(k=2.700\). So our equation is \(V=32,400-2,700t\). We must make sure that we actually answer the question, which asks for the value 4 years after it was purchased. If we plug \(t=4\) into our equation, we get \(V=32,400-2,700(4)\). So, \(V=21,600\). Correct Answer: A Again, looking at the answer choices indicates we will be dealing with equalities. Let’s see what information we can extract from the problem. Note that we are dealing with rectangular prisms, so you should have any relevant formulas on hand. The first constraint is that “the sum of the perimeter of the base of the box and the height of the box cannot exceed 130 inches.” This translates to \(P+h\:\leq\:130\), where \(P\) is perimeter and \(h\) is height. This sum must be less than or equal to 130, since 130 is the maximum possible sum allowed. Next, since the “perimeter of the base is determined using the width and length of the box,” and we know the base is a rectangle since we’re dealing with a rectangular prism, we have that \(P=2l+2w\), where \(l\) is the length and \(w\) is the width. This formula is given to you on the SAT, but it would be helpful to have it memorized. Substituting this new equation into our first one, we get: \(2l+2w+h\:\leq\:130\). The next constraints are that the height is 60 inches and the length is 2.5 times the width. This means \(h=60\) and \(l=2.5w\). If we plug this into our inequality, we have: \(2(2.5w)+2w+60\:\leq\:130\). When we simplify, \(w\:\leq\:10\). Because a measurement can never be negative, we also have that \(w\:\geq\:0\). So, \(0\:\leq\:w\:\leq\:10\), which corresponds to A. Correct Answer: C This problem also contains a lot of numeric information, so we should handle it one line at a time. First, we know that Ken earned $8 per hour for 10 hours of work. This means that Ken has already earned $80 dollars this week. Since Ken will now earn $10 for each additional hour of work, his total earnings for the week will be \(80+10h\), where \(h\) is the number of hours worked during the rest of the week. Since Ken saves 90% of these earnings, we have that his savings are: \(.9(80+10h)\). If we want to save “at least $270,” we must have that \(.9(80+10h)\:\geq\:270\). We can do algebra to solve for \(h\): \(80+10h\:\geq\:\frac{270}{0.9}\) \(80+10h\:\geq\:300\) \(10h\:\geq\:220\) \(h\:\geq\:22\) Correct Answer: 8 This problem requires knowledge of linear graphs, specifically the formula of a line and how to find a linear slope. From any two points \((x_1,y_1)\) and \((x_2,y_2)\), the slope of a line, \(m\), can be determined using \(m=\frac{y_2-y_1}{x_2-x_1}\). So, for our two points, \(m=\frac{0-4}{2-1}=-4\). This part of the problem is easy to mess up on, so make sure to double check your work here. So far, we have the equation \(y=-4x+b\) for our line, where \(b\) is the coordinate of the y-intercept. Now, we can pick one of the existing points on the line and plug in the values to find \(b\). Let’s use \((2,0)\). We have: \(0=-4(2)+b\). So, we get that \(b=8\). Correct Answer: A This problem can seem complicated, because having multiple variables might tempt students to solve for one at a time. However, the key to solving this problem is treating \(ax+b\) as just one variable. We can do this by factoring out 9: \(9(ax+b)-6=21\). Then, we can isolate \(ax+b\) on one side: \(9(ax+b)=21+6=27\) \(ax+b=27/9=3\) We can choose A as the answer. Correct Answer: A This problem may seem daunting given the length of the paragraph, but if we carefully read, we can see that the answer is more simple. The problem asks for what the y-intercept means. From our knowledge that the y-intercept occurs when \(x=0\), we know that the y-intercept occurs when the truck is driven 0 miles (since \(x\) represents miles driven). Because the total cost “consists of a flat fee plus a charge per mile driven,” if the number of miles driven is 0, the total cost in this situation is only equal to the flat fee. Thus, the y-intercept represents the flat fee, which corresponds to answer choice A. Correct Answer: C For this problem, I’d start by doing something familiar: finding the equation of the line. Since the line passes through \((0,0)\) and \((3,6)\) we can start by finding the slope: \(m=\frac{6-0}{3-0}=2\). So far, we have \(y=2x+b\) for the equation of our line. Next, we can use this slope and the point \((0,0)\) to construct an equation. Plug in \((0,0)\) into our equation, and we get \(0=2(0)+b\). So, \(b=0\) and \(y=2x\). So, for a point \((s,t)\) we have that \(t=2s\). This means that whatever \(s\) is equal to, \(t\) will be twice as much. It’s important to note that the question asks for the ratio of \(t\) to \(s\). Because \(t\) is twice as large as \(s\), the ratio should be 2:1. Correct Answer: B This question is a bit more complicated since it involves multiple variables. Again, the problem defines the variables for us. For a given food, the amount of calories is \(4p+9f+4c\), since we have 4 food calories for every 1 gram of protein, 9 food calories for every 1 gram of fat, and 4 food calories for every 1 gram of carbohydrate, according to the table. Since we were told the granola bar had 180 food calories, we can set our expression equal to this value: \(4p+9f+4c=180\). Since we want the equation in terms of \(f\), we now need to do some algebra to isolate for \(f\): \(4p+9f+4c=180\) \(9f=180-4p-4c\) \(9f=180-4(p+c)\) \(f=20-\frac{4}{9}(p+c)\) Correct Answer: 30 This situation may not seem like a linear system, since so little numeric information is given, but upon taking a closer look, we can extract additional information. First, let’s define \(C\) to be the number of correct answers and \(I\) to be the number of incorrect answers. Then, since any given question produces either a correct or incorrect answer, the total number of questions is \(C+I\). Next, the score is determined by “subtracting the number of incorrect answers from twice the number of correct answers.” So, the score is \(2C-I\). Since we are given that 40 questions were answered and the score is 50, we now have two equations: \(C+I=40\) \(2C-I=50\) We can solve this system by adding the two equations together: \(C+I+2C-I=40+50\) \(3C=90\) \(C=30\) We should make sure that the question was indeed asking for the number of correct answers (not the number of incorrect ones), and since it was, we are done. When approaching Heart of Algebra problems, remember to check to make sure you answered the question. The SAT will often anticipate common student errors and misconceptions and will construct the wrong answer choices based on them. So, it’s crucial that you make sure to answer the questions carefully, double checking your work if you have the time. The best way to study for the SAT Math section is to complete as many practice problems as you can. If you find yourself struggling on Heart of Algebra problems more than the other sections, try focusing your study solely on Heart of Algebra content. Check out some of these other posts to help you as you study for the SAT Math section: What’s Covered:
Overview of SAT Math Heart of Algebra
How Will the SAT Impact My College Chances?
Strategies to Solve Heart of Algebra Problems
10 Difficult Heart of Algebra Questions
1. System of Inequalities (No Calculator, Multiple Choice)

2. Constructing Linear Equations (No Calculator, Multiple Choice)


3. Geometric Application of Linear Inequalities (No Calculator, Multiple Choice)

4. Word Problems Involving Linear Equations (No Calculator, Multiple Choice)

5. Properties of Linear Graphs (No Calculator, Free Response)

6. Solving for Quantities within a Linear Equation (Calculator, Multiple Choice)
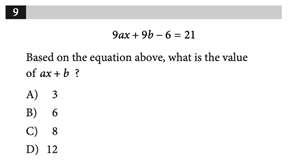
7. Real-World Applications of Linear Equations (Calculator, Multiple Choice)

8. Analyzing Linear Graphs (Calculator, Multiple Choice)
9. Constructing Multivariable Linear Equations (Calculator, Multiple Choice)

10. Creating and Solving a Linear System (Calculator, Free Response)

Final Tips and Strategies