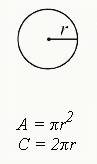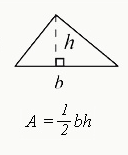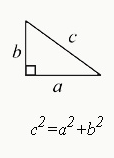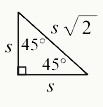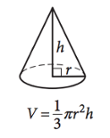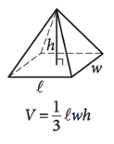Which Formulas Are Given on the SAT Math Section?

Preparing for the SAT can be a stressful experience for students and parents alike. After all, SAT scores can have a profound effect on a high schooler’s future success, impacting their ability to gain entry to top colleges and even win grants and scholarships. And with so much to study on both the reading and math sides of the test, families are often left feeling overwhelmed and at a loss for where to begin.
While SAT tutoring can help ease the burden, students should also do some independent digging to determine what information they do and don’t have to commit to memory before the big day. Read on to discover what formulas are given to students on the SAT Math section so that your student doesn’t waste time memorizing information that’s available to them during the exam.
Prepping for the SAT Math Section
The Math section of the SAT is designed to assess students’ understanding of those math concepts most likely to crop up in college. The current exam covers three different areas of math: Heart of Algebra, Problem Solving and Data Analysis, and Passport to Advanced Math. The goal is to determine whether students can apply what they’ve learned in high school to solve real-world problems through a combination of multiple-choice and gridded-response questions.
While the SAT is designed to measure what students already know, they don’t need to have every math concept and formula committed to memory in order to succeed. The College Board lists 12 of the most commonly used geometry formulas on every SAT Math section, so teens don’t need to stress over memorizing them all. Instead, high schoolers should devote valuable memory real estate to those algebra and trigonometry formulas not listed on the exam, and get comfortable on knowing where and when to use all of the above.
The Math Formulas on the SAT
Prepping for the SAT? The following 12 geometry formulas are listed on the SAT Math Sections:
1. Area of a Circle
A= πr²
This formula reveals that a circle’s area is equal to π (or 3.14159…) multiplied by the value of the radius of the circle (r) squared. The radius refers to any straight line drawn from the center point of the circle to the edge.
2. Circumference of a Circle
C=πd or 2πr
Used to calculate the circumference, or length around a circle, this formula reveals that C is equal to the value of π (or 3.14159…) multiplied by the diameter (d). Diameter refers to a line that bisects the circle through the midpoint.
3. Area of a Rectangle
A=lw
The area of a rectangle is equal to its length (l) multiplied by its width (w).
4. Area of a Triangle
A= 1/2 bh
Find the area of a triangle by multiplying the length of the base (b) by the length of the height (h), and then multiplying the total by 1/2.
5. The Pythagorean Theorem
a²+b²=c²
An important formula for solving geometry problems, the Pythagorean Theorem reveals that, for a right triangle, the sum of the squares of the two smaller sides is equal to the square of the larger side, known as the hypotenuse.
6. Properties of Special Right Triangle: Isosceles Triangle
H = s√2
This formula shows that, for isosceles right triangles, there is always a 90-degree angle and two 45-degree angles. Students can find the length of the hypotenuse (h) by multiplying the length of one of the two smaller sides (s) by the square root of 2.
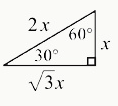
7. Properties of Special Right Triangle: 30, 60, 90 Degree Triangle
For 30, 60, 90 triangles, the length of the sides equal x, x multiplied by the square root of 3, and 2x respectively, with the side opposite the 30-degree angle having the small measurement.
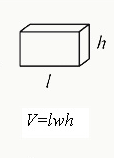
8. Volume of a Rectangular Solid
V=lwh
To calculate the volume of a rectangular solid, multiple the length of one side (l) by the height of the rectangle (h) and then multiply the total by the width of the figure (w).
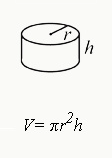
9. Volume of a Cylinder
V=πr²h
Find the volume of a cylinder by multiplying the radius (r) by the height (h) and then multiplying the result by π.
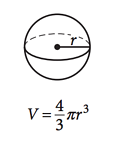
10. Volume of a Sphere
V=4/3 πr³
Calculate a sphere’s volume by multiplying the cube of the radius by π, and then multiplying the total by 4/3.
11. Volume of a Cone
V=1/3πr²h
The volume of a cone can be calculated by squaring the radius (r) of the cone’s circular component. Multiply this value by the height of the cone (h), as measured from the circular base. Finally, multiply the total by 1/3π.
12. Volume of a Pyramid
V=1/3lwh
The volume of a pyramid is equal to 1/3 multiplied by the length of the rectangular part of the pyramid (l), times the height of the pyramid at its peak (h), times the width of the edge of the rectangle (w).
Preparing for the SAT? Download our free guide with our top 8 tips for mastering the SAT.