Guide to SAT Passport to Advanced Math + Practice Questions
What’s Covered:
The SAT Math test is meant to evaluate your readiness for college-level math. However, regardless of your math skills in high school, you can achieve a high score on the math section of the SAT with enough concentrated, focused effort.
In this post, we’ll give you our best tips and strategies for tackling Passport to Advanced Math questions, as well as some practice problems you can tackle on your own!
Overview of the SAT Passport to Advanced Math Questions
The title of this section is self-descriptive, as these questions include topics that students should learn before studying advanced math. More specifically, they focus on linear equations, functions, and systems. Expect to encounter many polynomial equations in this section.
Since these questions tend to build on concepts covered in Heart of Algebra, it’s recommended that students develop proficiency on those questions before launching into the more advanced Passport questions.
This question type makes up around 16 out of the 58, or 28%, of the math questions you’ll see on test day. You may be asked to:
- Solve quadratic, linear, and polynomial equations.
- Define a term or constant and interpret your solution.
- Create and use quadratic and polynomial functions.
- Interpret graphs for quadratic and order-based functions.
- Use a preexisting graph to identify other equations in a system with a nonlinear equation.
- Create equivalent algebraic, quadratic, and/or exponential expressions.
- Rewrite simple expressions.
- Use function notation.
These questions are rather evenly dispersed throughout the test and their difficulty is randomized. There will be both multiple choice and free-response questions. While difficulty is subjective, many students struggle with this question type in particular. It’s a good idea to focus on your weaker areas while studying for any test, so if this one is yours, read on for tips and examples.
How Will the SAT Impact My College Chances?
With the exception of Covid years, most colleges have historically used the SAT and ACT as a predictor for college success. In fact, selective schools often use GPA and test scores as a filter, so if yours don’t make the cut, your application might not even be considered!
If you’re curious about how your scores might impact your shot at your stop schools, check out our free chancing engine! Our all-inclusive algorithm takes a deeply holistic approach, considering your stats, extracurriculars, and demographic information to give you the most accurate prediction possible. It’ll show you how you stack up in comparison to other applicants and even highlight areas for improvement!
Strategies for Passport to Advanced Math Questions
Work the multiple choice
Not all of these questions will be multiple choice, but the ones that are will be your best friend. When in doubt, you can often implement a process-of-elimination strategy, plugging in answers until you arrive at the correct one. This can get a bit time-consuming, however, so only do this if you can’t recall any other way of answering it, or if the other ways of answering will be even more time-consuming.
While looking through answer choices, a few might be clear non-answers right off the bat, so be sure to cross them off as soon as you notice them. That way, if you’re somehow left guessing, you’ll at least be choosing between 2 or 3 potential answers instead of 4, giving yourself much better odds.
This strategy only works when you’re saving yourself from little mistakes, however, so when crossing out answers and working through problems, be sure to note to yourself why exactly you’re doing so, so you aren’t just glossing through the work and making small mistakes without realizing it. Think of a time you’ve struggled to solve a math problem and turned to a friend to explain what you’ve done so far. You probably took them through your process, verbalizing each step as you went, before catching your mistake—like unthinkingly forgetting a negative sign or neglecting to carry a 1—on your own.
Similarly, you may have turned in a written assignment, only to look at it in the submission box and realize that your essay was riddled with little errors. By seeing your work in a different context, you more readily noticed your mistakes.
That’s because explaining and verbalizing situations can often force us to examine them more closely. While you can’t exactly talk out loud during a high-stakes standardized test, you can always try internally narrating your process to yourself to catch any little errors.
Know your exponent rules
Much of your success on this test will be based on your ability to implement universal math rules and procedures. You’ve probably been taught these in school, but if you’re a little rusty, here’s a refresher:
1. Don’t add or subtract bases. Bases are the “big number” in exponential expressions. For example, in the term \(3^2\), \(3\) is the base.
\(5^2 +7^2\) is not \(12^2\)! Since 5 and 7 are different values, they will produce different values when squared, tripled, etc.
2. Add the exponents when multiplying the same bases, and subtract them when dividing.
For example:
\(6^3(6^2) = 6^5\)
\(\frac{7^6}{7^3} = 7^3\)
This only works when the bases are the same!
Sometimes, you’ll have to do the inverse of this when distributing equations, especially with variables. For example:
\((xz)^3 = x^3\:\cdot\:z^3\)
This applies to roots as well, as roots are the same as exponents, just inverted:
\(\sqrt{xz} = \sqrt{x} \:\cdot\:\sqrt{z}\)
However, there’s a common mistake you should be sure to avoid. Sometimes students inappropriately distribute exponents and radicals like so:
\((x+z)^2 \:\neq\:x^2 + z^2\)
This is incorrect and easily avoided! This equation can be appropriately expressed like this instead:
\((x+z)^2 = (x+z)(x+z) = x^2+2xz+z^2\)
These rules can come in handy while simplifying equations (which we’ll get into later.) They can present a good way to break down a large number into smaller, simpler factors, like this:
\(\sqrt{72} = \sqrt{9}\:\cdot\:\sqrt{8}= 3\sqrt{8}\)
3. Multiply powers of powers
For example:
\((3^2)^3 = 3^6\). This does not equal \(3^5\).
4. Divide roots of powers
This works because roots are the inverse operation to powers.
\(\sqrt{x} = x^\frac{1}{2}\)
\(\sqrt[3]{x} = x^\frac{1}{3}\)
For example:
\(\sqrt{5^3} = 5^\frac{3}{2}\)
5. Know your negative exponents.
Negative exponents can be expressed as positive fractions.
For example:
\(x^{-1} = \frac{1}{x}\)
\(y^{-2} = \frac{1}{y^2}\)
6. And finally, any number to the 0 power is 1, without exception.
Remember that all of these rules also apply when using variables in these equations!
Understand equation structures
Learn the differences between linear, exponential, and polynomial equations, and be able to recognize each within a problem.
It’s also important to be aware of the different forms these equations can take. For example, quadratic equations can present in any of the following ways:
- Standard form: \(y = ax^2 + bx + c \)
- Factored form: \(y = a(x – x_1)(x – x_2)\), in which \(x_1\) and \(x_2\) are the x-intercepts, or zeroes.
- Vertex form: \(y = a(x + h)^2 + k\), in which \((h,k)\) is the vertex.
Similarly, linear equations can present in various ways, as follows:
- Slope-intercept form: \(y=mx+b\), in which \(m\) is the slope and \(b\) is the y-intercept.
- Point-slope form: \(y-y_1=m(x-x_1)\), in which \(m\) is the slope and \((x_1, y_1)\) is a given point on the line.
- Standard form: \(Ax+By = C\), in which A, B, and C are constants.
You’re most likely to come across slope-intercept form and point-slope form on the test.
In addition, we really recommend familiarizing yourself with FOIL and reverse FOIL equations (the latter of which can be used to find the x-intercepts, as can perfect squares).
Our other post, 30 SAT Math Formulas You Need to Know, explains these concepts and more in greater detail. It’s loaded with both descriptions of these formulas and suggestions on when to use them.
When studying for SAT Math, half the battle is familiarizing yourself with the content, while the other half is actually being able to recognize which information to actually apply when you’re taking the test. The latter skill is difficult to teach, and can really only be learned by doing. By taking practice tests, you’ll get better and better at noticing opportunities to draw from what you’ve learned.
Keep it simple, students!
Simplify virtually whenever possible and necessary. You’ll approach many equations that are absolutely loaded with terms that only serve as distracting noise. Combine like terms whenever possible while staying mindful of negative and positive signs, and you’ll find yourself looking at a much more consolidated, much more approachable equation.
10 Difficult Passport to Advanced Math Questions
Question 1

No calculator
Answer: C
Explanation:
This is one of those questions that is actually rather simple but just looks complex because of all of the unconsolidated terms.
To get rid of all of the parenthetical confusion, let’s distribute the negative sign.
\(( x^2y−3y^2 +5xy^2 ) − (−x^2y +3xy^2 −3y^2)\)
\(x^2y−3y^2 +5xy^2 +x^2y -3xy^2 +3y^2\)
Combine like terms:
\((x^2y+x^2y)+(−3y^2+3y^2)+(5xy^2−3xy^2)\)
\(= 2x^2y+2xy^2\)
Therefore, C is our answer. Any other answer would be incorrect and likely resultant of a failure to correctly combine like terms or a mistake with distributing the negative. Questions like these are a perfect example of how important it is to avoid little mistakes by honing your focus and taking each action with intention. Exponent rules came heavily into play here, so definitely brush up on these if they’re a weak area for you!
Question 2

No calculator
Answer: B
Explanation:
Since the right-hand side of the equation shows \(P\) being multiplied by a more complex expression, we can easily multiply each side by the reciprocal of this complex expression to isolate \(P\). Therefore, our final answer in terms of \(P\) is the reciprocal of the complex equation multiplied by \(M\).
A is incorrect because it is the result of multiplying each side by the original complex expression instead of by its reciprocal.
C is incorrect because it shows a false equivalency. \(\frac{r}{1200}\) is not equal to the reciprocal of the complex expression. A person who got this answer probably attempted to simplify the complex expression but made a few technical mistakes along the way.
D is incorrect for the same reason that C is.
Question 3

No calculator
Answer: B
Explanation:
Let’s simplify this equality by multiplying it by \(\frac{(x+2)(x+3)}{(x+2)(x+3)}\), which equals 1.
We’ll get \(\frac{(x+2)(x+3)}{\frac{(x+2)(x+3)}{x+2} + \frac{(x+2)(x+3)}{x+3}}\). After canceling like terms on the top and bottom, we get \(\frac{(x+2)(x+3)}{(x+3)+(x+2)}\). If we expand this equation, we get \(\frac{x^2+5x+6}{2x+5}\), which is equivalent to the answer shown in Choice B.
If you didn’t recognize how to solve this equation, you could also plug in a number larger than 3 and look for the answer that matches the value you get.
Question 4

Calculator allowed
Answer: D
Explanation:
This is a tricky one that will require a bit of process-of-elimination. So far, we have no clue if A, B, C, or D are correct, as we know nothing about how these expressions fit into the equation and aren’t given enough information to test them. D at least references the values we’ve been given so far.
This is what we do know:
If \(p(3) = -2\), then \(p(3)+2=0\). This basically means that if we were to shift the graph of \(p(x)\) up 2 units, then we would have a polynomial that’s divisible by 3, where \(x-3\) would be a factor of \(p(x)\). That means that when \(p(x)\) is divided by \(x-3\), we would be left with a remainder of \(-2\). Therefore, our answer is D.
Question 5
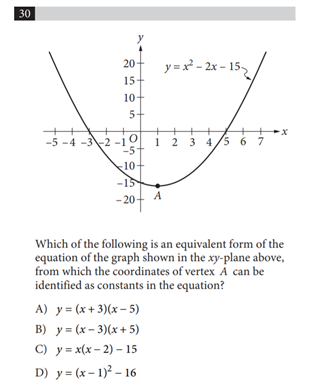
Answer: D
Explanation:
We need to find the vertex form of this equation, i.e. \(f(x) = a(x-h)^2 + k\), where a, h, and k are constants and \((h, k)\) is the vertex of the parabola when \(f\) is graphed in the coordinate plane.
Looking at the answer choices, D is the only option in vertex form, and the vertex coordinates \((1,-16)\) do look correct according to the graph.
To actually solve this question though, we need to find the vertex using math. In the form \(y=ax^2+bx+c\), the x-coordinate of the vertex is \(\frac{-b}{2a}\). For our equation \(y = x^2-2x-15\), the x-coordinate of the vertex is then \(\frac{-(-2)}{2(1)}=1\). We can plug this value into the equation as \(x\) to find the y-coordinate. We get \(y=(1)^2-2(1)-15=1-2-15=-16\).
So, the vertex is in fact located at \((1, -16)\), and the vertex form of this equation is:
\(y = (x-1)^2 -16\)
Therefore, the answer is D.
Question 6

Answer: A
Explanation:
Let’s start by setting the two equations equal to one another to find the x-coordinates of the intersecting points:
\(25 = (x-11)^2\)
Logically, this means that \(x-11 = 5 \) or \(-5\), as you would get that answer if you were to square both sides.
\(x-11 = 5\)
\(x = 16\)
\(x- 11 = -5\)
\(x = 6\)
Therefore, the points are \(A = (16, 25)\) and \(B=(6, 25)\). Since the points have the same y-coordinate, we don’t need to use the distance formula and can instead subtract 6 from 16 to get a length of \(\overline{AB}=10\). You should, however, know the distance formula between two points \((x_1, y_1)\) and \((x_2, y_2)\) for the SAT: \(\sqrt{(x_2-x_1)^2-(y_2-y_1)^2}\).
Therefore, the distance between point A and point B is 10, making A the correct answer. B, C, and D are all incorrect and likely resulted from an arithmetic error. Possible mistakes may include misusing negative and positive signs, using the wrong value for \(x\), or not using the method outlined here altogether.
Question 7

No calculator
Answer: 9
Explanation:
All we need to do is simply!
\((-3x^2 + 5x-2)-2(x^2-2x-1)\)
\(-3x^2+5x-2-2x^2+4x+2\)
\(-5x^2 + 9x +0\)
\(b\), the coefficient of the value of \(x\), is 9, so the answer is 9.
Question 8

Calculator allowed
Answer: D
Explanation:
To decrease the present population by 10 percent, it must be multiplied by \(0.9\). Since this will happen every 20 years, \(50,000\) must be multiplied by \((0.9)^n\), in which \(n\) represents the number of 20 year periods that will have elapsed \(t\) years from now.
We can use fraction \(\frac{t}{20}\) to represent this number of 20-year periods and stand in for \(n\). Therefore, \(50,000(0.9 )^\frac{t}{20}\) represents the engineer’s estimate of the population of the city \(t\) years from now, so D is correct.
A is incorrect because it multiplies 50,000 by 0.1, which would decrease the present population by 90%, all the way down to 10% of its original size. In addition, the exponent is incorrect, as it is the product of 20 and the number of 20 year periods that would elapse over time.
B is incorrect because it multiplies 50,000 by 0.1, which would decrease the present population by 90%, all the way down to 10% of its original size.
C is incorrect because its exponent is incorrect, as it is the product of 20 and the number of 20 year periods that would elapse over time.
Question 9
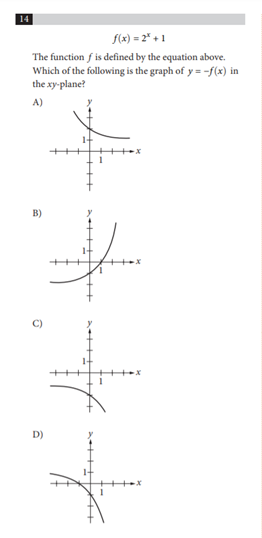
No calculator
Answer: C
Explanation:
Let’s employ some process of elimination strategies!
First, let’s think about what we know about \(y = -f(x)\), or \(y = -2^x -1\)
\(f(x)\) is a positive function, so \(-f(x)\) must be a negative function. That immediately rules out Choices A and B.
Secondly, substitute \(0\) in for \(x\) to find the equation’s y-intercept.
\(y = -2^0 -1 = -1-1 = -2\)
We now know that the function has to pass through \((0,-2)\), and Choice C is the only option that does so.
Choice D is incorrect because it does not pass through this point and passes through \((0,-1)\) instead. Students may miss this one because of faulty algebra.
Question 10
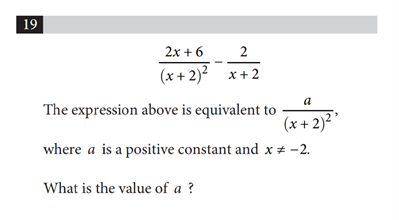
No calculator
Answer: 2
Explanation:
To find \(a\), make the denominators the same in the above expression, as the numerator will then be equivalent to \(a\). To do this, multiply \(\frac{-2}{x+2}\) by \(\frac{x+2}{x+2}\).
We get \(\frac{-2(x+2)}{(x+2)^2}=\frac{-2x-4}{(x+2)^2}\)
So our final expression is \(\frac{2x+6}{(x+2)^2} + \frac{-2x-4}{(x+2)^2}\)
This simplifies to \(\frac{2x+6-2x-4}{(x+2)^2}= \frac{2}{(x+2)^2}\)
Therefore, \(a=2\)
Final Tips and Strategies
With enough practice and strategy, you can give yourself a significant leg up in your test-taking journey. Aside from this, however, learn to manage your time while taking the test.
Since all questions are worth the same, go ahead and skip the ones you have no clue how to answer and come back to them later. Don’t do this before experimenting with a couple of mathematical strategies first, though!
And if you’re still at a loss, remember that there is no guessing penalty, so an educated guess is better than no answer at all! You won’t lose points for a wrong answer.
If you’re still on the lookout for more SAT math help, check out these articles:
SAT Math: How to Handle Word Problems