How To Tackle Circle Problems on the SAT Math Test
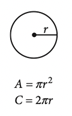
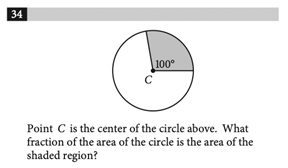
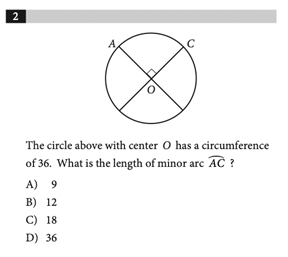
Radius, circumference, tangency – if you are unfamiliar with these terms, you should definitely brush up on your knowledge of circles! The SAT expects you to be familiar with the properties of circles, and you’ll probably encounter a few circle problems on the math portion of the exam. This post will cover important circle concepts and show solutions with explanations for a few sample problems! The SAT Math Test consists of a No-calculator and Calculator section. The No-calculator section gives 25 minutes to complete 20 questions and the Calculator section gives 55 minutes for 38 questions. Questions involving geometry often appear on the SAT Math Test; when it comes to circles, you will be expected to understand their fundamental properties and equations. Most circle problems on the SAT are associated with a picture, and ask you to solve for a specific value. However, sometimes the problems only consist of text. To best solve these kinds of problems, mark up the diagrams as much as you can, and if a diagram is not given, draw your own! Pictures help you better contextualize the information and solve for unknowns. The SAT gives the following formulas and information regarding circles: We recommend memorizing this information, as it will save you the time of constantly flipping back to the front of the test. Also, having this information handy can help guide you when you’re unsure of how to approach a problem. Here are some important properties of circles that you should know. If you’re unfamiliar with any of the below topics, be sure to look at the associated problems, and complete additional practice SAT problems involving circles to get a better handle on them. Every circle can be defined by its radius or diameter. Equivalent sized circles will have equivalent radii. The radius is the distance from the center of the circle to the edge of the circle. The diameter is the length of a line connecting two edges of the circle and passing through the center. The diameter is equal to twice the radius. The radius of a circle is important because it’s used to compute properties such as the circumference and area, which we’ll cover in more detail later. You probably won’t get tested on just the radius or diameter, but you’ll likely encounter a problem that will require knowledge of these two properties. Some of the problems we’ll look at later will involve these concepts. The circumference of a circle is its perimeter. In other words, it’s the total length of the boundary of the circle. The SAT gives the formula to calculate the circumference, \(C=2\pi r\), where \(r\) is the radius of the circle. Again, it’s best to have this formula memorized to make circle problems on the SAT easier. The SAT gives you the information that the number of degrees in a circle is \(360^{\circ}\), and the number of radians is \(2\pi\). From this, you can easily convert from radians to degrees, using the fact that \(360^{\circ}=2\) rad. Here’s a problem that asks for a conversion: Answer: 4 To solve this problem, let’s start with what’s given, \(720^{\circ}\). We can set up a conversion factor as follows: \(720^{\circ}\:\cdot\:\frac{2\pi\:rad}{360^{\circ}}\) We put degrees on the bottom and radians on the top so that the degrees cancel and we are left with radians, which is what we want. Simplifying the above expression yields \(4\pi\), so we know that \(a=4\). Knowing the total number of degrees in a circle allows us to solve problems involving area. The area of a circle is the measure of the total space within the boundary. Like circumference, a formula is given for the total area of a circle: \(A=\pi r^2\). Rather than have you directly compute the area given a known radius, the SAT will probably ask a more conceptual question like the one below: Answer: 5/18 For this problem, you should know that the proportion of degrees corresponds directly to the proportion of the area. So, since the shaded region is \(100^{\circ}\), it constitutes 100/360, or 5/18, of the total circle. This fraction is based off of the fact that the total number of degrees in a circle is \(360^{\circ}\). So, this problem required conceptual knowledge of area, and the formula for area was not needed. Another important component of a circle is arcs. An arc is a portion of the circumference of a circle, and can be measured in degrees. To better understand arcs, take a look at this problem: First, let’s define minor and major arcs. When looking at \(\overset{\frown}{AC}\), the minor arc is the shorter path between them. The major arc is the longer path between them. So, when looking at minor arc \(\overset{\frown}{AC}\), we notice that the angle between the segments \(\overline{AO}\) and \(\overline{CO}\) is a right angle, so minor arc \(\overset{\frown}{AC}\) measures \(90^{\circ}\). Like with area, the proportion of degrees corresponds to the proportion of the circumference. So, in this case, since the minor arc measures \(90^{\circ}\), its length corresponds to 90/360, or 1/4, of the total circumference of a circle. Therefore, since the circumference is 36, the length of the minor arc is 1/4 of that, or 9. To do well on the SAT Math Test, you should be familiar with equations of circles. Unlike the other formulas, this is not included at the beginning of the test. Equations of circles take the following form: \((x-h)^2+(y-k)^2=r^2\), where \((h,k)\) is the coordinates of the center of the circle and r is the radius. You should memorize this equation and be familiar with the form. Most SAT problems involving the equation of a circle rely heavily on algebra, like the following: Answer: A The equation given is not in the proper form, so we’ll need to use complete the square to get it into the proper form. When given an expression of the form \(x^2+bx\), adding the term \((\frac{b}{2})^2\) will result in a perfect square trinomial, which can be simplified to \((x+\frac{b}{2})^2\). Let’s do this for both \(x\) and \(y\). We can first divide the total expression by 2 to eliminate the coefficients next to \(x^2\) and \(y^2\). This gives us \(x^2-3x+y^2+y=\frac{45}{2}\). We can now complete the square: So, we have \(x^2-3x+(\frac{-3}{2})^2\) and \(y^2+y+(\frac{1}{2})^2\). These expressions simplify to: \(x^2-3x+\frac{9}{4}\) and \(y^2+y+\frac{1}{4}\). If we are adding \(\frac{9}{4}\) and \(\frac{1}{4}\) to the left side of the equation, we must also add these to the right side to keep things balanced. We get: \(x^2-3x+\frac{9}{4}+y^2+y+\frac{1}{4}=\frac{45}{2}+\frac{9}{4}+\frac{1}{4}\). This simplifies to \((x-\frac{3}{2})^2+(y+\frac{1}{2})^2=25\), which is the proper form we were looking for. Since the right side of the equation of a circle is \(r^2\), we have that \(r^2=25\), so \(r=5\). Circles have many important associated angles. The following problem illustrates some of the types of angles associated with circles. Answer: 80 Here, we have two important types of angles. \(\angle{BAC}\) is an inscribed angle and \(\angle{BPC}\) is a central angle. The measure of the central angle is always twice the measure of the inscribed angle, if they intercept the same arc. In the problem, \(\angle{BAC}\) and \(\angle{BPC}\) both intercept the \(\overset{\frown}{BC}\). To find the value of \(x\), we’ll need to find the measure of \(\angle{BAC}\). Finding this will require knowledge of radii and triangles. Line segments \(\overline{AP}\), \(\overline{BP}\), and \(\overline{CP}\), are all radii of this circle, and are therefore equivalent. Since \(\overline{AP}\) and \(\overline{BP}\) are equivalent, \(\bigtriangleup APB\) is an isosceles triangle. Therefore, \(\angle{ABP}\) and \(\angle{BAP}\) are also equivalent and both equal \(20^{\circ}\). With this same logic, \(\angle{PAC}\) also equals \(20^{\circ}\). Since \(\angle{BAP}\) and \(\angle{CAP}\) together add up to \(\angle BAC\), we know that the measure of \(\angle{BAC}\) is \(20^{\circ}+20^{\circ}=40^{\circ}\). So, the measure of \(\angle{BPC}\) should be twice the measure of \(\angle{BAC}\), and is \(80^{\circ}\). The unit circle is a special circle with important properties. Questions involving the unit circle fall under the category Additional Topics in Math, which constitutes about 10%, or 6 questions, of the SAT Math test. Most unit circle problems can be solved using trigonometry, but having the unit circle memorized will make such problems much easier and faster to solve. Here is what the unit circle looks like: The Academic Index (AI) is a metric used by selective colleges to assess a student’s academic profile. A student’s AI is calculated from data such as their GPA and standardized test scores, including the SAT and ACT. The AI is an important factor in the college admissions process, since some schools will even automatically reject an applicant with a too low of an AI. To see how your SAT score stacks up against other applicants, use CollegeVine’s free Admissions Calculator. This tool will not only determine your chances at your dream schools, but also inform you of which other aspects of your profile need to be improved! What’s Covered:
Overview of the SAT Math Test

Properties of Circles + Practice Questions
Radius/Diameter
Circumference
Degrees/Radians

Area

Arcs
Answer: AEquation of a Circle
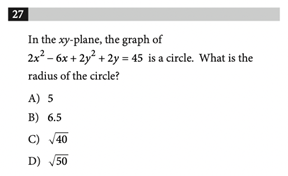
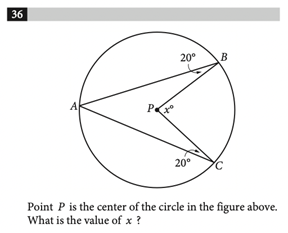
Angles
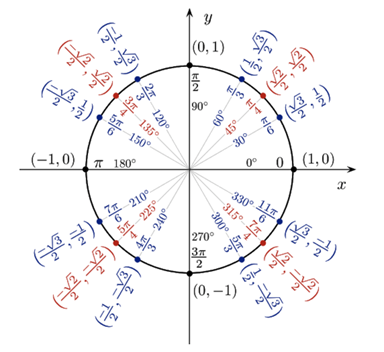
The Unit Circle
How Will the SAT Impact My College Chances?