The Unit Circle: What You Need to Know for the SAT

You may recall committing the unit circle to memory in your math class, or maybe you’re currently learning it and wondering if you’ll ever see this topic outside a classroom setting. Will it show up on the SAT, and how will knowing (or not knowing) it affect your score? Read on to find out.
What is the Unit Circle?
The unit circle is a trigonometric concept that allows mathematicians to extend sine, cosine, and tangent for degrees outside of a traditional right triangle. If you recall, sine, cosine, and tangent are ratios of a triangle’s sides in relation to a designated angle, generally referred to as theta or Θ.
- Sine is the ratio of the length of the opposite leg of the right triangle over length of the hypotenuse.
- Cosine is the ratio of the length of the adjacent leg of the right triangle over the length of hypotenuse.
- Tangent is the ratio of the length of the opposite leg over the length of the adjacent leg.
Using these traditional definitions, we are limited to describing the angles we find in right triangles, which are between 0 and 90 degrees. In some instances, we need to know these values for angles larger than 90, and the unit circle makes that possible.
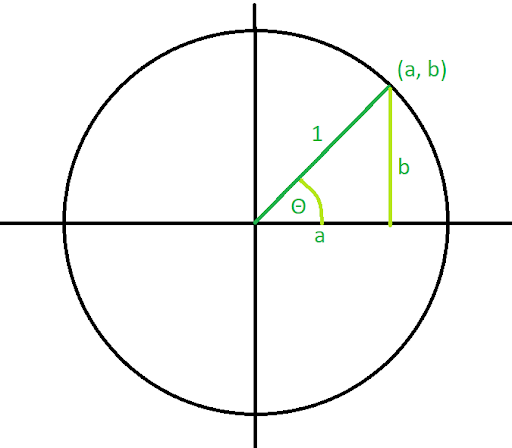
The unit circle is so named because it has a radius of 1 unit. Its center is at the origin, and all of the points around the circle are 1 unit away from the center. If we draw a line from the center to a point on the circumference, the length of that line is one (as shown below). We can then add a line to create a right triangle, where the height is equal to the y-coordinate and the length is equal to the x-coordinate. These measures are marked a and b respectively. The point on the circle is thus (a, b).
The values for a and b depend on the angle; in the example above, we’d need to find (or know) the degree from the positive x-axis to the terminal side marked in dark green. But we can use the above circle to find out the general relationship of a and b to any degree within the circle.
Using our standard trig definitions above, we can find the cosine and sine of theta. Cosine is adjacent over hypotenuse, or a/1. This reduces to just being a. Sine is opposite over hypotenuse, or b/1. Again this reduces to simply b. The point (a,b) above can be rewritten as (cos Θ, sin Θ). In fact, this holds true for any point on the unit circle where you create an angle using a terminal side. We can now find the sine and cosine for angles equal to 0 or larger than 90.
Although this is true for any angle on the unit circle, most math teachers (and the SAT) focus on the points created by the 45-45-90 right triangle and the 30-60-90 triangle (using 30 and 60). Since we now have the measure of Θ (either 30, 45, or 60) we can find the cosine and sine for each of these angles according to the unit circle.
Before we move onto showing the full unit circle, let’s talk about radians. Radians are used to measure the arc of a circle caused by the terminal side (marked in dark green above). The circumference of the unit circle can be found quickly using the standard circumference formula, which is 2πr. The radius is 1, which means that the circumference of the unit circle is 2π.
Let’s imagine the terminal side starting at the positive x-axis on the right and rotating about the origin counterclockwise, not unlike the hand of a clock but backwards. When it reaches the positive x-axis again, it will have completed a 360 degree rotation. Thus, 360 degrees corresponds to 2π (or the entire circumference). Every other point is correspondingly less than 2π in proportion to the number of degrees the terminal side has moved from the starting position on the right.
We can now use the ratio to convert degrees to radians and vice versa. If we are given degrees, we can multiply it by 2π/360. If we are given radians, we can multiply the value by 360/2π.
Here’s the unit circle you know and love. Each quadrant follows the patterns described above. 
Do You Need to Know it for the SAT?
As one of the main tests used in admissions, the SAT can test on anything covered in high school math classes. Therefore, there’s a chance that the unit circle will appear on the SAT you end up taking.
That said, the unit circle is not frequently tested, and many of the problems involving the unit circle can be solved through other means (just like most problems on the SAT can be solved in multiple ways). According to the College Board, the unit circle falls under the category Additional Topics in Math, which only accounts for 10%, or 6 questions, on the entire Math Test. That’s 6 questions spread out between both the calculator and no-calculator sections.
Additional Topics in Math tends to favor a few other math subjects before it gets to the unit circle and radians, such as:
- Lines and angles
- Triangles and other polygons
- Circles (from a geometrical standpoint)
- Area and volume
- Coordinate geometry (equations of lines and circles in the coordinate plane)
- Basic trigonometry
- Complex numbers.
As you can imagine, the test makers aren’t always able to jam all of the above topics and the unit circle into six questions, though these questions do at times draw upon two or more topics in order to solve. Some of the College Board’s free practice tests do not feature a single question requiring knowledge of the unit circle.
That said, if you want a perfect score on the SAT Math Test, you should feel confident in virtually any topic that the SAT might throw on their test, including the unit circle. You don’t want to neglect a topic only to find, as luck would have it, that it appears on the particular test you take.
If you aren’t aiming for perfection but are still going for a good score, you may want to focus on areas of math that are always tested on the SAT or are more commonly tested. To learn more about the topics tested on the SAT Math, check out our post What Does the Math Section of the SAT Test?
Sample Questions and Tips
All of these sample questions come from the College Board’s free practice tests. We’ve included at least one way to solve each of these problems, but each can be solved through a few different methods.
No calculator, gridded response question
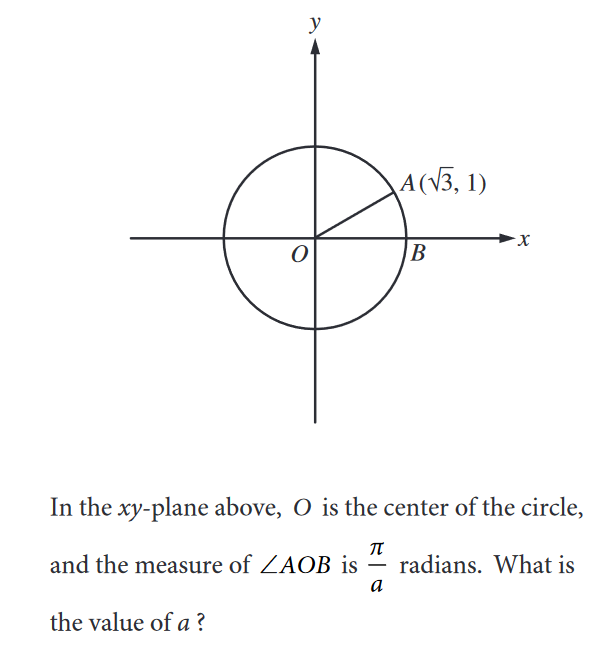
How to solve: If you’ve memorized the unit circle, then you won’t need to do any calculations because you’ll be able to spot the relationship between the coordinates. They correspond to the 30-degree angle, which corresponds to π/6. The answer is thus 6.
Alternate method: If you remember that the coordinates correspond to the cosine and sine of the angle made by the terminal side, you can figure out the degrees of the angle. You can draw the right triangle and label it, using the x-value as the length of the long side and the y-value as the length of the short side.
You may then recognize that it’s a 30-60-90 triangle, or you may solve for the hypotenuse using the Pythagorean theorem to find that it follows the 30-60-90 triangle pattern. This gives you the angle measure 30, which you can convert to radians by multiplying it by 2π/360. You’ll get 60π/360, which reduces to π/6. The answer is 6. (Don’t be tempted to put 360 as your answer. You know you need to reduce because the value is given as π/a, where π has no coefficient.)
Calculator allowed, gridded response

How to solve: The area of the sector to the area of the circle is proportionate to the length of the arc (measured in radians) to the circumference of a circle in radians. Remember that a full circle measures 2π radians, and figure out what fraction 5π/4 is out of 2π.
Set 5π/4 over 2π as a fraction, as in:
\(\frac{\frac{5\pi}{4}}{2\pi}\)
You can rewrite this as division:
\(\frac{5\pi}{4}\div2\pi\)
Now, change the division to multiplication by multiplying the first fraction by the reciprocal of the second.
\(\frac{5\pi}{4}\cdot\frac{1}{2\pi}\)
You’ll end up with 5π/8π. The π can actually be eliminated (because π is not actually a variable, but a constant) so you are left with 5/8.
Helpful Tips
If you plan on mastering the unit circle for that perfect SAT Math section score, then keep in mind the following. Many of these tips apply to all math questions as well!
Don’t over-rely on your calculator. As you can see, the unit circle could show up on either the no-calculator portion or the calculator portion. You should practice working with the unit circle without a calculator so that you can be prepared if it shows up on the no-calculator section.
Know the concepts; don’t just memorize. Memorizing the unit circle can help you solve a problem super quickly, as in the first example where having it memorized meant you didn’t have to do any calculations. However, if you understand the patterns, and know how the coordinates relate to the sides of a triangle and trigonometric functions, you can use more tools to help you solve more complex problems.
Preparing for the SAT? Download our free guide with our top 8 tips for mastering the SAT.
For more help with SAT Math, check out these posts below:
Which Formulas Are Given on the SAT Math Section?
5 Common SAT Math Mistakes to Avoid
Want to know how your SAT score/ACT score impacts your chances of acceptance to your dream schools? Our free Chancing Engine will not only help you predict your odds, but also let you know how you stack up against other applicants, and which aspects of your profile to improve. Sign up for your free CollegeVine account today to gain access to our Chancing Engine and get a jumpstart on your college strategy!