Ultimate Guide to the AP Calculus BC Exam 2024
What’s Covered:
- When is the AP Calculus BC Exam
- About the AP Calculus BC Exam
- AP Calculus BC Exam Structure
- AP Calculus BC Score Distribution, Average Score, and Passing Rate
- How to Study for the AP Calculus BC Exam
In 2023, approximately 409,000 of the over 5 million students taking AP exams, or 8%, took an AP Calculus exam. Most of these students took the AP Calculus AB exam, which covers pre-calculus along with differential and integral calculus, but about 135,000 took the AP Calculus BC exam, which goes into deeper detail, by covering the same content plus polar coordinates, sequences and series, vectors, and an introduction to differential equations.
If you’re planning to take the AP Calculus BC exam, whether you have taken the class or self-studied, read on for a breakdown of the test and CollegeVine’s advice for how to best prepare for it.
When is the AP Calculus BC Exam?
The 2024 AP Calculus BC exam is on Monday, May 13, at 8 am local time.
About the AP Calculus BC Exam
Much like Calculus AB, AP Calculus BC focuses on the unifying themes of calculus, including derivatives, integrals, limits, approximation, applications and modeling, and sequences and series, as well as practical applications of these concepts. Computation is important, but the real emphasis of the course is on a multidimensional approach to calculus.
In other words, concepts will be tested in a wide range of ways. Problems could involve analysis of graphs, numbers, or word problems. You will also be asked to evaluate the relationships between various functions, and use technology to deepen your understanding of those connections.
The AP Calculus BC course is broken down into two separate components that students must master in order to demonstrate an understanding of calculus and pass the AP Calculus BC exam. The two key components are mathematical practices and big ideas.
Mathematical Practices
Mathematical practices are the four key skills a student must possess to complete the tasks asked on the AP Calculus exam. The practices of the AP Calculus BC course are:
| Mathematical Practice | Description |
Percentage of Exam Score (Multiple-Choice Section) |
Percentage of Exam Score (Free-Response Section) |
| Implementing Mathematical Processes | Determine expressions and values using mathematical procedures and rules | 53%-66% | 37%-59% |
| Connecting Representations | Translate mathematical information from a single representation or across multiple representations | 18%-28% | 9%-16% |
| Justification | Justify reasoning and solutions | 11%-18% | 37%-59% |
| Communication and Notation | Use correct notation, language, and mathematical conventions to communicate results or solutions | N/A | 9%-20% |
Big Ideas
The other key component of the AP Calculus BC curriculum is big ideas. Big ideas are the foundational concepts and themes that run throughout the course, which will ideally come together to provide you with a deeper overall understanding of calculus, and math as a whole. The three big ideas of the AP Calculus course are:
| Big Idea | Description |
| Change | The integration and differentiation as expressed in the Fundamental Theorem of Calculus—a central idea in AP Calculus |
| Limits | Beginning with a discrete model and then considering the consequences of a limiting case allows us to model real-world behavior and to discover and understand important ideas, definitions, formulas, and theorems in calculus |
| Analysis of Functions | Calculus allows us to analyze the behaviors of functions by relating limits to differentiation, integration, and infinite series and relating each of these concepts to the others |
AP Calculus BC Course Content
Of course, the AP Calculus BC exam is based on the material covered in the course itself. As an advanced course, the AP Calculus BC curriculum requires a good deal of foundational knowledge, whether you enroll in the course or self-study. You will need four years of high school level mathematics, with a deep understanding of algebra, geometry, trigonometry, analytic geometry, and functions before you enroll in AP Calculus BC.
In terms of functions specifically, which are really the backbone of this course, you should be familiar with linear, polynomial, rational, exponential, logarithmic, trigonometric, inverse trigonometric, and piecewise-defined functions. It’s also valuable to have some knowledge of the properties of functions, the algebra of functions, the graphs of functions, and the language of functions.
In addition, because this course goes into more complex mathematical concepts than AP Calculus AB, you should ideally have basic knowledge of sequences and series, as well as some exposure to polar equations.
The AP Calculus BC course is broken down into 10 individual units. Below is a list of these units, and how much weight each one is given on the exam.
| Unit | Percentage of Exam Score (Multiple-Choice Section) |
| Limits and Continuity | 4%–7% |
| Differentiation: Definition and Fundamental Properties | 4%–7% |
| Differentiation: Composite, Implicit, and Inverse Functions | 4%–7% |
| Contextual Applications of Differentiation | 6%-9% |
| Analytical Applications of Differentiation | 8%–11% |
| Integration and Accumulation of Change | 17%–20% |
| Differential Equations | 6%–9% |
| Applications of Integration | 6%–9% |
| Parametric Equations, Polar Coordinates, and Vector-Valued Functions | 11%–12% |
| Infinite Sequences and Series | 17%–18% |
Calculators
You will need access to a scientific graphing calculator for the duration of AP Calculus BC, including on the exam. Your calculator should be able to plot the graph of a function within an arbitrary viewing window, find the zeros of functions, numerically calculate the derivative of a function, and numerically calculate the value of a definite integral.
You will be allowed to use your calculator on one part of the multiple-choice section and on one part of the free-response section. Don’t panic too much about the no-calculator sections, though. Questions in those sections will be more theoretical, and will require only relatively basic calculations. In other words, they are designed to be solved without a calculator—you are not being set up to fail.
More information and a list of acceptable calculator models can be found in the official Calculator Policy.
AP Calculus BC Exam Structure
The AP Calculus BC exam is one of the longest AP exams, clocking in at three hours and 15 minutes. Like other APs, though, the exam is divided into two primary sections: one section of multiple-choice questions, and the other made up of free-response questions.
Section 1: Multiple Choice
1 hour 45 minutes | 45 questions | 50% of score
The first section takes one hour and 45 minutes, contains 45 multiple-choice questions, and accounts for 50% of your total score. This section has two separate parts. Part A consists of 30 questions, lasts for 60 minutes, and makes up 33.3% of your exam score. In this section, you will not be allowed to use your calculator. You may use your calculator on Part B, which contains 15 questions, lasts for 45 minutes, and makes up 16.7% of your exam score.
Here’s an example of a multiple-choice question that you’re not allowed to use a calculator to answer:
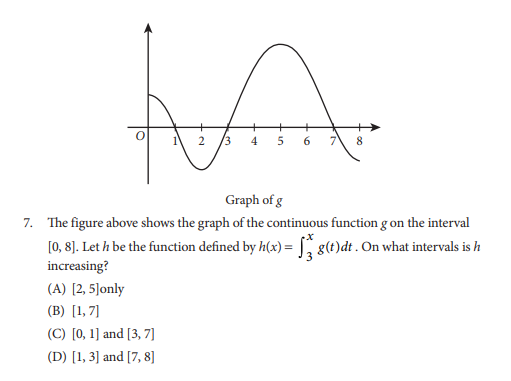
Source: The College Board. Answer: C
Here’s an example of a multiple-choice question that you are allowed to use a calculator to answer:
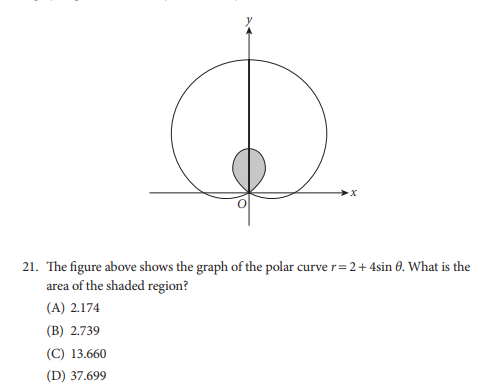
Source: The College Board. Answer: A
Section 2: Free Response
1 hour 30 minutes | 6 questions | 25% of score
The free-response section is next, which lasts for one hour and 30 minutes, and accounts for the remaining 50% of your score. Like the multiple-choice section, the free-response section is split into two parts. Part A contains two problems, which you will have 30 minutes to complete, with the use of your calculator, and is worth 16.7% of your exam score. Part B has four problems, which you will have 60 minutes to complete, without the use of your calculator, and is worth 33.3% of your exam score.
Here’s an example of a free-response question that you are allowed to use a calculator to answer:

Source: The College Board.
Here’s an example of a free-response question that you’re not allowed to use a calculator to answer:
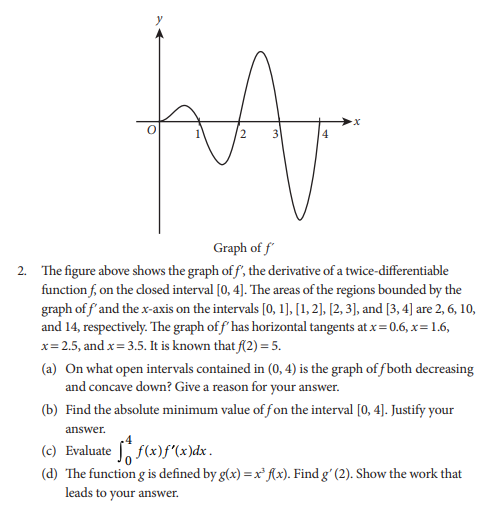
Source: The College Board.
AP Calculus BC Score Distribution, Average Score, and Passing Rate
| Score | 5 | 4 | 3 | 2 | 1 |
| Students | 43.5% | 15.9% | 19% | 15.2% | 6.3% |
Perhaps counterintuitively, given the complexity of the content test, students generally perform quite well on the AP Calculus BC exam. However, given the course’s stringent guidelines for prerequisite knowledge, most students who enroll are already well-suited to handle its rigor. In other words, the students who take this exam in the first place are somewhat self-selecting.
In 2023, the average score on this exam was a 3.75, almost 80% of students earned a passing score (3 or above), and less than 7% received the lowest score of 1.
Keep in mind, though, that policies on credit and advanced placement based on AP scores vary widely from school to school. Though a score of 3 is typically considered passing, it is not always enough to receive credit, especially at more selective institutions. The College Board’s website will allow you to check which score(s) you’ll need at the schools you’re considering to receive credit for AP Calculus BC.
How to Study for the AP Calculus BC Exam
Step 1: Assess Your Skills
You will need to begin your studying with some measure of your current knowledge. Although the AP Calculus BC course was redesigned in the 2016-2017 school year, its content has remained almost entirely the same, which is a good thing when it comes to sourcing practice exams and study materials, as you can rely on previous administrations of the exam when assessing yourself.
The College Board has made the 2012 exam and the 2008 exam available. There are also diagnostic and practice tests provided in many test prep books, and your teacher may have additional sample tests, or even real exams from past years, at their disposal.
Step 2: Study the Material
AP Calculus BC focuses on differential and integral calculus, along with sequences and series. You will need to demonstrate your knowledge of limits, derivatives, definite integrals, and the Fundamental Theorem of Calculus to perform well on the exam.
You’ll also need to be confident dealing with a series of numbers, power series, and various methods to determine convergence or divergence of a series. For example, you will need to be familiar with Maclaurin series for common functions, and general Taylor series representations.
Make sure you practice with various kinds of problems—remember, the concepts could be presented graphically, numerically, analytically, and verbally. You should also be able to use your calculator to help solve problems, experiment, interpret results, and support conclusions.
For a more specific idea of where to focus your studying, you may consider using a commercial study guide. The Princeton Review’s prep book for 2024 includes a complete, updated guide to the exam, chapter reviews, practice problems, and three practice tests. Another solid choice is Barron’s AP Calculus which covers both AB and BC calculus content in a concise and accurate way.
There are also a number of free study resources available online. Because calculus is a popular AP choice, many teachers and students have experience with the exam already, and may have posted study materials online to help those currently enrolled in the course. One study guide/calculus resource can be found on Lamar University’s website, but there are many others out there.
Finally, remember that your classmates and teacher can be fantastic resources as well. Explaining a concept to someone else is often the best way of evaluating how well you know it yourself, or your peers may be able to explain an idea in a way that makes more sense to you than the textbook, and your teacher is always there to clarify any especially tricky topics.
Step 3: Practice Multiple-Choice Questions
After you gain a solid understanding of the basic theory required on the exam, test your knowledge by practicing multiple-choice questions. Most study guides provide practice multiple-choice questions, or you can find more through online searches.
For example, you could try taking the multiple-choice section of another practice exam. The College Board provides a set of sample questions with scoring explanations and there are several study books available that consist entirely of multiple-choice questions with answers.
One highly rated book is Multiple Choice Questions to Prepare for the AP Calculus BC Exam: 2021 AP Exam Preparation Workbook. Another great option is the collection of multiple-choice questions available online through Khan Academy.
The College Board course description also includes many practice multiple-choice questions, along with explanations of their answers. As you go through these, try to keep track of which areas are still tripping you up, and go back over the relevant theory again. Keep a running list of the concepts that you need more practice with.
Step 4: Practice Free-Response Questions
The free-response portion of the AP Calculus BC exam will test your ability to solve problems using an extended chain of reasoning. In this section, you will be expected to demonstrate sound mathematical reasoning and thinking to support your answer. An answer without supporting work will receive no credit.
Each part of the free-response section is timed, and you may use a graphing calculator only for Part A. During Part B, you cannot use a calculator.
Even when using a calculator, though, take care to show all of your work on the free-response section. There should be a clear record of every step you took to arrive at your solution. If you use your calculator to solve an equation, compute a numerical derivative, or find a definite integral, be sure to write the equation, derivative, or integral down, not just enter it into your calculator.
The College Board has the free-response questions from the AP Calculus BC exam dating back to 1998 posted on their website. In addition to the questions themselves, the College Board also provides scoring commentary, which is extremely useful for understanding how much work the exam graders are expecting you to show.
Step 5: Take Another Practice Test
Once you’ve completed the steps above, take another formative assessment. Varsity Tutors offers a handful of free diagnostic tests and practice exams. Another resource is Study.com, which offers a range of practice questions for free, as well as numerous full-length practice exams if you make an account.
Taking regular practice tests will help you keep track of your progress, as well as identify which areas are still causing you trouble and adjust your approach accordingly, to ensure you’re using your study time as productively as possible. If you repeat the steps listed above between practice tests, you should see your score slowly but steadily increase.
Step 6: Exam Day Specifics
The day before your AP Calculus BC exam, prepare everything you’ll need, then focus on doing some mindfulness exercises, listening to your favorite music, or relaxing in some other way, before getting a good night of sleep. Studies show these steps are far more likely to result in a strong performance than last-minute cramming!
How Will AP Scores Affect Your College Chances?
While AP scores themselves don’t play a major role in the college admissions process, having AP classes on your transcript can be a crucial part of your application, especially at highly selective institutions. College admissions officers want to see that you enjoy challenging yourself intellectually, and that you’re capable of handling college-level coursework, and taking AP classes demonstrates both of those qualities.
The main benefit of scoring high on AP exams comes once you land at your dream school, as high scores can allow you to “test out” of entry-level requirements, often called GE requirements or distribution requirements. This will save you time and money.
If you’re starting to think about what schools you should apply to, we recommend that you use CollegeVine’s free chancing engine. This tool will consider your test scores, GPA, extracurriculars, and more, to calculate your chances of acceptance at various schools and to help you decide where to apply. It can also give you suggestions for how to boost your chances of acceptance—for example, by taking more AP classes in your junior or senior year.


