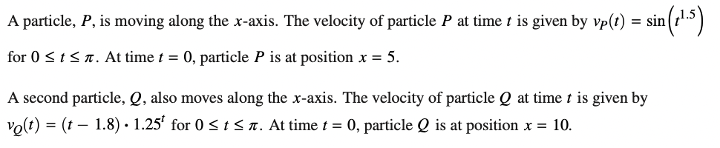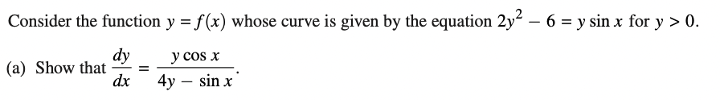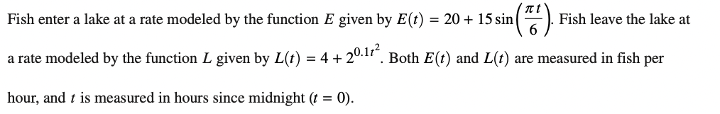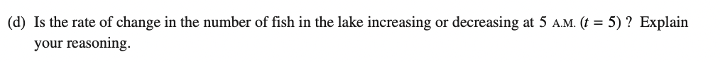How to Tackle the AP Calculus AB Free Response
With just over half of students receiving a passing score on the AP Calculus AB exam, you’ll need to make sure you have a good handle on the free response portion to do well on this test. The free response section of the AP Calculus AB exam contains a variety of questions, and each one is involved and requires you to have a strong command of calculus. In this post, we’ll cover how best to tackle the free response section and provide plenty of practice problems, along with detailed explanations of how to solve them.
How Will AP Scores Impact My College Chances?
AP scores actually don’t factor into your college admissions chances! Instead, admissions committees look to see that you’ve taken the hardest courses available at your high school (whether that be AP, IB, honors, or whatever else your school offers). This doesn’t mean that you shouldn’t try on your exams, however – receiving a passing score might mean that you receive college credit or place out of introductory courses.
If you want to see how your course rigor compares to other applicants, check out CollegeVine’s free Admissions Calculator. This calculator will consider your GPA, test scores, classes, extracurriculars, and more to determine your admissions chances at whichever schools you’re applying to.
Overview of the AP Calculus AB Exam
The AP Calculus AB Exam tests your ability to understand and apply calculus concepts.
The exam format is as follows:
Section I: Multiple Choice, 50% of exam score
- No calculator: 30 questions (60 minutes)
- Calculator: 15 questions (45 minutes)
Section II: Free Response, 50% of exam score
- Calculator: 2 questions (30 minutes)
- No Calculator: 4 questions (60 minutes)
For the free response section, each question is scored out of a total of nine points, and you should aim to get an average of at least 5 to 6 points per question to receive a high score on the overall exam.
AP Calculus AB Free Response Tips
Here are some general guidelines to keep in mind as you prepare for the AP Calculus AB Free Response Exam.
Don’t simplify your answers
The AP Calculus AB Exam Free Response section does not require you to simplify your answers. For example, if you’re computing a definite integral without a calculator, you can leave your answer like this:
\(5(4)^2 + 2(4) – 36 – (5(0)^2+2(0)-36)\)
This might be counterintuitive since you may not be used to leaving your answers unsimplified, but leaving your answers like this will still receive full credit! It’s better to leave your answer unsimplified than to simplify your answer and risk making a careless computation mistake. Especially for questions in which you don’t have your calculator, make sure to leave your answers unsimplified whenever possible to maximize your chances of receiving full credit.
Use correct units and label your responses
This exam actually requires that you use correct units! So, make sure to include units whenever applicable. Take the extra time to review your answers and ensure you have all the correct units – this way, you don’t risk losing a point or two from a correct solution just because you forgot to include the units.
Also, try to label your responses as much as possible. If you’re solving for a maximum or minimum within a multi-step problem, label “Solving for the maximum and minimum” before writing out the solution. Remember, the graders are attempting to understand your methodology and way of thinking. What’s intuitive to you might not be intuitive to them; so, be as clear as possible with your solutions so that they understand what you’re doing.
Justify completely
Rather than checking whether your numbers are correct or not, the graders are instructed to look at the justification of your answers. Simply stating that the answer will not give you full credit on the question. You need to justify how you got your answer in order to attain all nine points.
Pay attention to notation
You should be very careful of the notation when you’re writing out your solutions. You can lose points just for setting up an incomplete integral.
For example, \(\int_2 5x^2 dx\) would likely not receive full credit since it’s missing the upper bound.
Therefore, as you practice for this exam, pay extra attention to notation in order to lessen the chance of making mistakes.
AP Calculus AB Free Response Practice Questions
The types of free response questions that you’ll encounter on this exam can be broken down into eight different categories. We’ll cover what each category looks like, along with how best to approach each type of question. Each practice question is taken from a past official AP exam.
1. Area and Volume Problem
It’s more likely that you’ll encounter this type of problem on the no calculator portion of the exam, but there is a chance it’ll be on the calculator portion. In either case, you’ll need to be extra careful when setting up the integrals. Make sure you have the right notation, including upper and lower bounds.
These questions may require you to set up integrals to solve for:
- Area
- Volume
-
- Rotated around the x-axis
- Rotated around the y-axis
- Rotated around the line x=k
- Rotated around the line y=k
- Cross sections
Here is a sample problem:
Answer: \(\bf{c=\sqrt{\frac{15}{32}}}\)
We are told that the spinning toy has the shape of the solid generated by rotating that curve about the \(x\)-axis.
If we can determine the radius of the revolved solid, \(r\), then we can set up the following equation:
\(V=\pi\int r^2 dx\)
First, let’s determine the bounds of our integral. When we analyze the curve \(y=cx\sqrt{4-x^2}\), we see that it intersects with the \(x\)-axis at \(x=0\) and \(x=2\). So, our bounds are from \(0\) to \(2\).
Next, let’s determine our radius. If we were to visualize the region being revolved around the \(x\)-axis, we can see that the radius would be the height of the curve. So, we have that:
\(r=cx\sqrt{4-x^2}\)
Now, let’s set up our integral, set it equal to \(2\pi\), and solve for \(c\):
\(V= \pi \int_0^2 (cx\sqrt{4-x^2})^2 \ dx\)
\(= \pi \int_0^2 c^2 x^2 (4-x^2) \ dx\)
\(= \pi c^2 \int_0^2 4x^2 – x^4\)
\(= \pi c^2 [\frac{4x^3}{3}-\frac{x^5}{5}]_0^2\)
\(= \pi c^2 [\frac{4(2)^3}{3}-\frac{2^5}{5}]\)
Now that our expression only contains \(c\), we can set it equal to \(2\pi\) and solve:
\(2\pi = \pi c^2 [\frac{4(2)^3}{3}-\frac{2^5}{5}]\)
Solving for \(c\), we get:
\(c=\sqrt{2/[\frac{4(2^3)}{3}-\frac{2^5}{5}]}\)
Because we can leave answers unsimplified, the above answer would receive full credit.
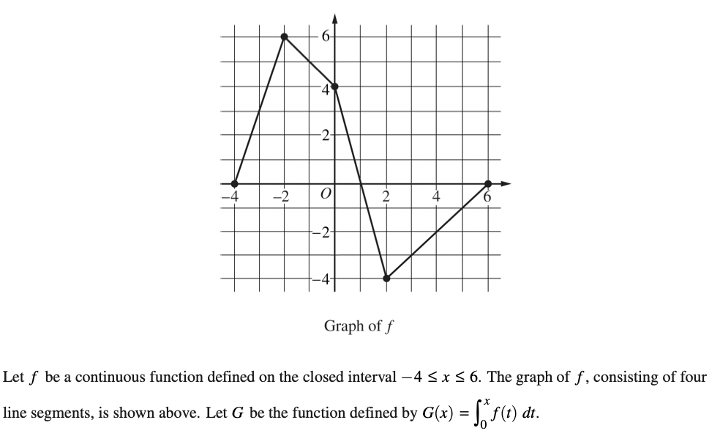
2. Analyzing a Graph of a Derivative
This type of free-response will always involve a graph.
The graph could be given in a few different formats:
- \(f'(x)\), the derivative of a given function \(f(x)\)
- \(v(t)\), the velocity of a particle and the derivative of \(x(t)\)
- \(f(x)\), where \(g(x)=\int_c^x f(t) \ dt\)
In any case, you’ll need to analyze the graph carefully and look for points where it changes slope or crosses the \(x\)-axis.
Let’s take a look at a practice free-response problem:
Answer: \(\bf{P'(3)=5.5}\)
To find \(P'(3)\), we’ll first need to define \(P'(x)\).
Using the product rule, \(P'(x)=G'(x)f(x)+G(x)f'(x)\)
So, \(P'(3)=G'(3)f(3)+G(3)f'(3)\).
Let’s find each part individually:
\(G'(x)\) is actually just equal to \(f(x)\), since \(G(x)=\int_0^x f(t) \ dt\). So, \(G'(3)=f(3)=-3\), from the graph.
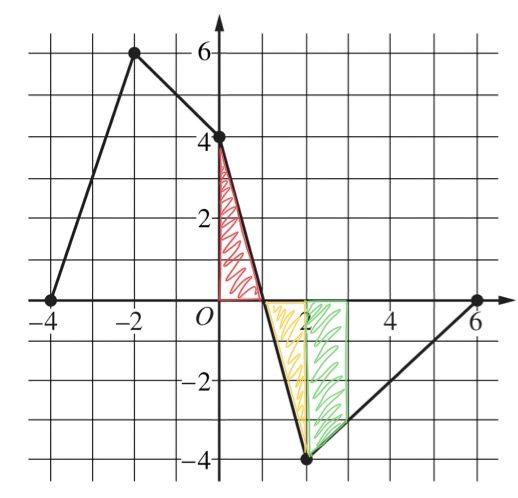
\(G(3)=\int_0^3 f(t) \ dt\), which is just the area under the curve of \(f\) from \(0\) to \(3\). If we split the area up from 0 to 1, then 1 to 2, then 2 to 3, we have two triangles and a trapezoid:
So, \(G(3) = \frac{1}{2}(4)(1) – \frac{1}{2}(4)(1) – \frac{1}{2}(4+3)(1) = -3.5\). Note that we subtract the second two areas since the curve is below the x-axis.
Finally, \(f'(3)=1\), because the slope of the graph at \(x=3\) is \(1\).
Putting the pieces together, we get that:
\(P'(3)=(-3)(-3)+(-3.5)(1)=5.5\)
3. Particle Problem
For these problems, you’ll usually be given velocity and an initial position. With that information, you might be asked to determine the position or acceleration of the particle at a specific time, whether the particle is speeding up or slowing down, displacement or the total distance traveled.
Remember these facts as you approach these problems:
- The derivative of position is velocity, and the derivative of velocity is acceleration. In other words, \(x'(t)=v(t)\) and \(x”(t)=v'(t)=a(t)\).
- The particle is speeding up when \(v(t)\) and \(a(t)\) are the same sign. The particle is slowing down when \(v(t)\) and \(a(t)\) are opposite signs.
- The displacement is: \(\int v(t) \ dt\)
- The total distance traveled is: \(\int |v(t)| \ dt\)
Let’s try a sample problem:
Answer: 1.931
This problem is fairly straightforward. We’ll need to use the given formula to solve for total distance traveled.
Total distance = \(\int_o^\pi |v_P (t)| \ dt = \int_0^\pi |\sin{t^{1.5}}| \ dt\)
Because this is a calculator problem, we can simply input this into our calculator to get that the total distance traveled by particle \(P\) is 1.931. Remember to always round to 3 decimal places.
4. Implicit Differentiation and/or Variable Separable
For these problems, be very careful when differentiating and integrating. Pay attention to the chain rule and any lingering constants.
Let’s solve this practice problem:
This question is nice in that it already gives us the answer – we simply need to show the steps to get there. So, let’s differentiate this equation step by step, then solve for \(\frac{dy}{dx}\). Recall that everytime you see a constant that is not associated with a variable, it becomes 0. Also, wherever you differentiate \(y\), you’ll need to include the term \(\frac{dy}{dx}\):
\(2y^2 – 6 = y\sin{x}\)
\(4y\frac{dy}{dx} – 0 = \sin{x}\frac{dy}{dx} + y\cos{x}\)
\(4y\frac{dy}{dx} – \sin{x}\frac{dy}{dx} = y\cos{x}\)
\(\frac{dy}{dx} = \frac{y\cos{x}}{4y-\sin{x}}\)
5. Equation(s) given as Rates of Change
For these problems, remember that if an equation is given to you as a rate of change, then it’s a derivative. So, you’ll need to take the integral to find the total amount, and you’ll need to take the derivative to determine if the rate of change is increasing or decreasing.
Let’s look at this practice problem:
Answer: Decreasing
Remember that it’s not enough to simply state that it’s decreasing. We’ll need to fully justify our answer. To determine whether the rate of change is increasing or decreasing, we’ll need to take the derivatives of the given equations.
First, let’s define an equation for the rate of change. We say that \(R(t)=E(t)-L(t)\). This is because fish enter at the rate of \(E(t)\) and leave at the rate of \(L(t)\), so we’ll need to subtract \(L\) from \(E\).
Now, we take the derivative: \(R'(t)=E'(t)-L'(t)\). But, we want to know if it’s increasing or decreasing at \(t=5\), so let’s plug in \(5\).
Using our calculator, \(R'(5)=-10.722\). Because this amount is negative, we see that the rate of change is decreasing at \(t=5\).
6. Analyze a Table of Values
When analyzing a table of values, pay close attention to labels. Make sure you understand what information is being given to you. Also, it may be helpful to draw a quick sketch of what the graph would look like to help you determine the relationship between the variables.
You’ll likely be asked to set up a Riemann sum for these types of problems. So, make sure to note whether you’re being asked for the left endpoints, right endpoints, midpoints, or trapezoids.
This sample problem illustrates how to approach table problems:
Solution: f'(2.25) = 8
To estimate \(f'(2.25)\), remember that the derivative is just the slope of the tangent line. So, to estimate this slope, let’s look at the line which connects the points to the left and right of 2.25. Then, we’ll use that line’s slope to estimate \(f'(2.25)\).
The points that we’re interested in are \((2,6)\) and \((2.5,10)\). Let’s find the slope of the line connecting these two points:
\(m = \frac{10-6}{2.5-2} = 8\)
But, we’re not done here! We need to explain the meaning of this answer within the context of the problem. First, note that \(f(r)\) is the density of a bacteria population, given in milligrams per square centimeter. So, \(f'(r)\) is the rate of change of the density of a bacteria population, given in milligrams per square centimeter per square centimeter.
Then, \(f'(2.25)=8\) means that at a distance of \(r=2.25\) centimeters from the center of the petri dish, the density of the bacteria population is increasing at a rate of 8 milligrams per square centimeter per centimeter.
7. Slope Fields
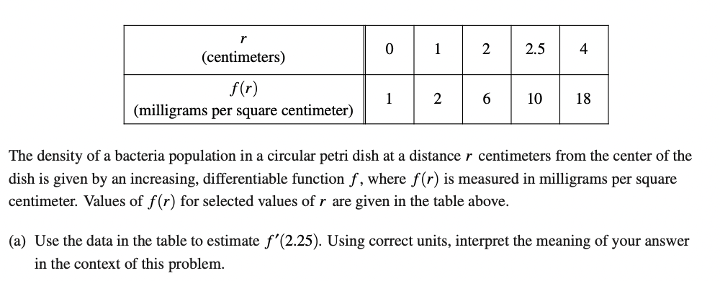
While slope fields might be on the more confusing side conceptually, in practice the problems can actually be fairly simple.
Let’s jump right into a sample problem:
When sketching the solution curve, it’s actually pretty intuitive. Make sure to start at the given point, then follow the lines from there. We see that towards the top of the graph we have a line of horizontal slopes, which means there’s likely an asymptote at that point.
Then, a solution curve could look like:
Note that the graph follows the asymptote. Also, the curve should be strictly increasing and concave down, because of the given \(\frac{dy}{dt}\) equation.
8. Related Rates
These problems can become complicated very quickly. To keep yourself organized, make sure to actively read the problem to determine what you know and don’t know. Before you start the problem, write down what you know. Then, write down what you need to find. Then, set up your equations and solve for the unknown (you’ll usually have to differentiate at some point).
Let’s tackle a practice problem:
Answer: \(\bf{\frac{dV}{dt}=\frac{-\pi}{5}}\) cubic feet per second
Let’s start with what the problem gives us. Note that we want everything in terms of radius \(r\), height \(h\), volume \(V\), and time \(t\).
Since the diameter is \(2\) feet, we have that the radius is \(1\) foot, or \(r=1\).
Next, we have that \(\frac{dh}{dt}=\frac{-1}{10}\sqrt{h}\) and \(V=\pi r^2 h\).
Because we want the rate of change of volume, let’s start with differentiating our volume equation:
\(V=\pi r^2 h\)
\(\frac{dV}{dt} = \pi r^2 \frac{dh}{dt}\) (Note that we can treat \(r\) as a constant since it doesn’t change with respect to time.)
Let’s plug in what we know to solve for \(\frac{dV}{dt}\):
\(\frac{dV}{dt} = \pi (1)^2 (\frac{-1}{10}\sqrt{h})\)
To finish this problem, recall that we’re solving for the rate of change of volume when the height is \(4\) feet, so let’s plug in \(h=4\).
\(\frac{dV}{dt} = \pi (1)^2 (\frac{-1}{10}\sqrt{4}) ft^3 /s\)
Once again, this unsimplified answer would receive full credit. Also, make sure to include units, or you risk losing points!
Additional Resources
As you study for the AP Calculus AB exam, check out some of CollegeVine’s other relevant guides: