10 Hardest AP Calculus AB Practice Questions
With about 60% of students passing in 2020, the AP Calculus AB Exam is pretty tough. This test is one of the longer ones, and takes a total of 3 hours and 15 minutes. As with any math test, the key to this exam is practice! In this article, we’ll go over some of the harder questions you may encounter on the exam, along with detailed explanations of how to solve them. AP scores themselves actually don’t carry much weight in the application process. Applications don’t require you to report your scores, and if you do self-report them, they don’t really boost your chances of admission. What colleges do look for, however, are the classes themselves. Taking AP classes in high school demonstrates your course rigor and shows colleges that you’re challenging yourself. Taking these classes and getting good grades in them proves to schools that you’re ready for the academic rigor of college classes. To see how your AP classes and course rigor affect your chances, take a look at CollegeVine’s free Admissions Chances Calculator. This tool will consider your test scores, GPA, extracurriculars, and more to predict your chances at the schools you’re interested in, and will even offer tips and guidance for how best to improve your profile! The AP Calculus AB exam will be offered both on paper and digitally in 2021. The paper administration is held on May 4, 2021 and May 24, 2021: The digital administration is held on June 9, 2021: For the digital exam, a calculator is allowed on all sections. The AP Calculus AB course is organized into 8 units. The units are listed below, along with their weighting for the multiple choice section of the exam: Here are some tough AP Calculus AB Questions for you to look over. Answer: B You’ll definitely need to understand limits and their properties for the AP Calculus AB exam. For this particular question, we can start by trying to plug in \(\pi\). For the numerator, we get: \(\cos(\pi)+\sin(2\pi)+1=-1+0+1=0\). For the denominator, we get: \(x^2-\pi^2=0\). Since we have a 0 in both the numerator and denominator, we’re able to use L’Hospital’s rule, which means we’ll need to take the derivative of the numerator and denominator, separately. Taking the derivative of the numerator yields: \(-\sin(x)+2\cos(2x)\). Also, the derivative of the denominator is: \(2x\). So, our limit now becomes: \(\lim_{x \to \pi} \frac{-\sin(x)+2\cos(2x)}{2x}=\frac{-\sin(\pi)+2\cos(2\pi)}{2\pi}=\frac{0+2(1)}{2\pi}=\frac{2}{2\pi}=\frac{1}{\pi}\), which means our answer is B. Answer: C When it comes to continuity, an easy rule of thumb is to check whether you can draw the graph without lifting your pencil. In this case, the graph only has one interruption, at \(x=0\). So, \(f\) is continuous at all points besides \(x=0\). Since \(f\) is discontinuous at \(x=0\), answer choices B and D are incorrect (since the question asks where \(f\) is continuous but isn’t differentiable). So, either A or C is correct, which means we need to check differentiability at \(x=1\) and \(x=-2\). At \(x=1\), we have a corner, so \(f\) is not differentiable at \(x=1\). Also, at \(x=-2\), we have a vertical tangent, and \(f\) is therefore not differentiable at \(x=-2\). Then, answer choice C is correct. Answer: A Questions involving slope fields tend to involve a lot of guess and check. For this question, we can start by looking at key \(x\) and \(y\) values. First, if we look along the \(y\)-axis, we see that the slope is \(0\). So, regardless of our \(y\)-value, if \(x=0\), we should have that \(\frac{dy}{dx}=0\). For A, if we plug in \(x=0\), we get: \(\frac{dy}{dx}=0y+0=0\). For B, if we plug in \(x=0\), we get: \(\frac{dy}{dx}=0y+y=y\). For C, if we plug in \(x=0\), we get: \(\frac{dy}{dx}=y+1\). For D, if we plug in \(x=0\), we get: \(\frac{dy}{dx}=(0+1)^2=1\). So, we see that the only equation which has tangent slopes of \(0\) along the \(y\)-axis is the one that corresponds to choice A. Answer: B Recall that the average value of a function \(f\) on the interval \([a,b]\) is given by the formula: \(f_{avg}=\frac{1}{b-a} \int_{a}^b f(x)dx\). So, we’ll need to compute the integral of \(f\) over \([-4,4]\). Since we’re given a graph, we can do this by calculating the areas of different sections. We can divide up the graph into triangles and trapezoids: Range Shape Area \((-4,-2)\) triangle \(\frac{1}{2}(2)(1)=1\) \((-2,1)\) triangle \((1,3)\) triangle \(\frac{1}{2}(2)(2)=2\) \((3,4)\) trapezoid \(\frac{1}{2}(1+2)(1)=3/2\) Keep in mind that the value from \((-2,1)\) is negative since the function lies below the \(x\)-axis. To compute the integral, we can add up all our values: \(\int_{-4}^4 f(x)dx=1-3+2+3/2=3/2\). But, we’re not done yet! We still need to multiply by \(\frac{1}{4-(-4)}=1/8\). So, the average value is \((1/8)(3/2)=3/16\). Answer: D These questions are really easily missed when students fail to apply chain rule. When we find \(f'(x)\), we’ll need to be careful to apply chain rule. Let’s set \(F(x)=\int_{1}^x \frac{1}{1+\ln{t}}\). Then, \(f(x)=F(x^3)\). So, \(f'(x)=F'(x^3)\). But, when we differentiate \(F(x^3)\), we’ll need to apply chain rule and multiply by the derivative of \(x^3\). This means that \(F'(x^3)=(F(x^3))'(x^3)’\). So, \(f'(x)=F'(x^3)=\frac{1}{1+\ln{x^3}}\cdot3x^2\). Then, \(f'(2)=\frac{1}{1+\ln{2^3}}\cdot3(2)^2=\frac{12}{1+\ln{8}}\). [amp-cta id="9459"] Answer: D Recall the following formula used when converting integrals to limits: \(\int_{a}^b f(x)dx=\lim_{n \to \infty}\sum_{k=1}^n f(a+(\frac{b-a}{n})k)\cdot\frac{b-a}{n}\). So, in this case, we have that \(a=3\), \(b=5\), and \(f(x)=x^4\). Also, \(b-a=2\). Then, \(\int_{3}^5 x^4dx=\lim_{n \to \infty}\sum_{k=1}^n (3+\frac{2k}{n})^4\cdot\frac{2}{n}\), which corresponds to choice D. Answer: A To solve the differential equation \(\frac{dy}{dt}=ky\), we’ll first need to divide both sides by \(y\) and multiply both sides by \(dt\). This yields \(\frac{dy}{y}=k\:dt\). Since we’ve separated our variables \(y\) and \(t\), we can now integrate: \(\int \frac{dy}{y}=\int k\:dt\). \(\ln{y}=kt+C\). To isolate for \(y\), we’ll need to put both sides as a power of \(e\): \(e^{\ln{y}}=e^{kt+C}\) \(y=e^{kt+C}=e^{kt}\cdot e^{C}=e^{kt}\cdot C=Ce^{kt}\). We can now use a point from the table, \((0,4)\) to solve for \(C\): \(4=Ce^{k(0)}\) \(4=C\). This means that \(y=4e^{kt}\). To solve for \(k\), let’s use another point from the table, \((2,12)\): \(12=4e^{k(2)}\) \(3=e^{2k}\). Let’s take the natural log of both sides: \(\ln{3}=\ln{e^{2k}}\) \(\ln{3}=2k\) \(k=\frac{1}{2}\ln{3}\). So, we get that \(y=f(t)=4e^{\frac{t}{2}\ln{3}}\). Answer: D You should expect to be asked to interpret information on the AP Calculus AB exam. For this question, since \(H(t)\) is the temperature of a room (in ºF) \(t\) minutes after a thermostat is adjusted, \(H'(t)\) would be the change in the temperature of the room per minute, \(t\) minutes after the thermostat is adjusted. So, if \(H'(5)=2\) means that 5 minutes after the thermostat is adjusted, the change in temperature is 2 ºF per minute. Since 2 is positive, the temperature is increasing, and D is the correct answer choice. You may be tempted to pick answer B, but it states that “the temperature of the room increases by 2 degrees,” which talks about a single event rather than the rate of change. Answer: B Though this question allows the use of a calculator, we’ll still need to do quite a few calculations by hand. First, recall the relationship between position, velocity, and acceleration: \(x”(t)=v'(t)=a(t)\). So, to get to the position function, we’ll need to integrate acceleration twice. \(v(t)=\int a(t)\:dt=\int -6t^2-t\:dt=-2t^3-\frac{1}{2}t^2+C\). From the problem, we know that at time \(t=0\) seconds, the velocity of the car is \(80\) meters per second. So, we can use that \(v(0)=80\) to solve for \(C\). \(v(0)=-2(0)^3-\frac{1}{2}(0)^2+C=80\Rightarrow C=80\). This question is tricky since we aren’t given both our bounds. We know the time period starts at \(t=0\) and ends at the moment the race car stops. To find the time that the race car stops, we’ll need to set \(v(t)=0\) (since if the car is stopped, the velocity should be \(0\) meters per second). We can do this by graphing the velocity function and finding the zeros. If we graph \(y=-2x^3-\frac{1}{2}x^2+80\) we see that the zero is \(3.339\). Now, using our calculators, we can integrate the absolute value of the velocity function to determine the distance travelled from \(t=0\) to \(t=3.339\): \(\int_{0}^{3.339} |-2t^3-\frac{1}{2}t^2+80|\:dt=198.766\). Note that we integrated the absolute value to determine the total distance travelled. Integrating just the velocity function gives us the displacement of the race car. Answer: A For related rates problems, it’s helpful to start with a familiar formula. In this case, since we’re given information about the volume of a sphere, let’s use that formula: \(V=\frac{4}{3}\pi r^3\) Now, we can differentiate with respect to time, \(t\): \(\frac{dV}{dt}=4\pi r^2\cdot \frac{dr}{dt}\) We know that \(\frac{dV}{dt}=2\pi\) and \(r=5\), so we can solve for \(\frac{dr}{dt}\): \(2\pi =4\pi (5)^2 \cdot \frac{dr}{dt} \Rightarrow \frac{dr}{dt}=1/50\). Next, we’ll need to use the surface area formula: \(S=4\pi r^2\) Again, we differentiate with respect to time \(t\) to find the rate at which the surface area is decreasing when the radius is 5 meters: \(\frac{dS}{dt}=8\pi r \cdot \frac{dr}{dt}\) We can plug in the appropriate values of \(r\) and \(\frac{dr}{dt}\) to find \(\frac{dS}{dt}\). \(\frac{dS}{dt}=8\pi (5)(1/50)=4\pi /5\). Especially on the digital exam, you’ll be using your calculator a lot. Knowing your calculator well will help you get through questions much more quickly. For example, some calculus questions may be able to be solved without the use of a calculator, but there are many cases where using a quick calculator trick during intermediate steps will save you a significant amount of time. Since the AP Calculus AB exam requires you to answer many questions in limited time, it’s imperative that you learn to properly pace yourself. So, when answering practice questions, try to time yourself in a format that’s similar to the exam (i.e. give yourself 1 hour and 45 minutes to answer 45 multiple choice questions). This will help you practice your pacing and if you find that you’re struggling to finish on time, you can rethink your strategy. Since all the multiple choice questions carry equal weight, skipping difficult or time-consuming problems is more beneficial for you. Check out these other articles as you prepare for your AP exams: What’s Covered:
How Will AP Scores Impact My College Chances?
Overview of the AP Calculus AB Exam
10 Hardest AP Calculus AB Questions
Question 1

Question 2
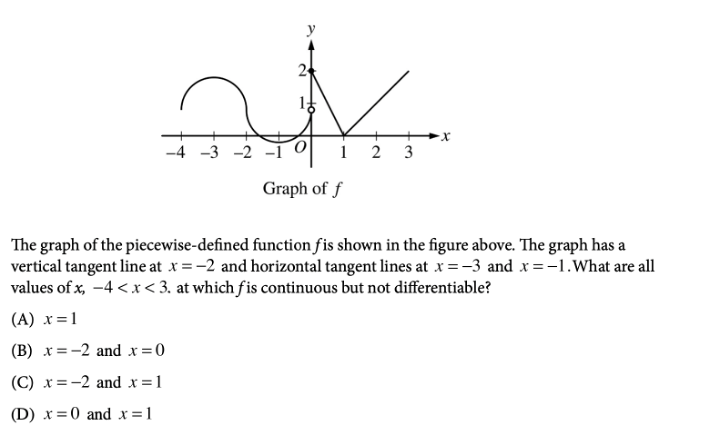
Question 3

Question 4
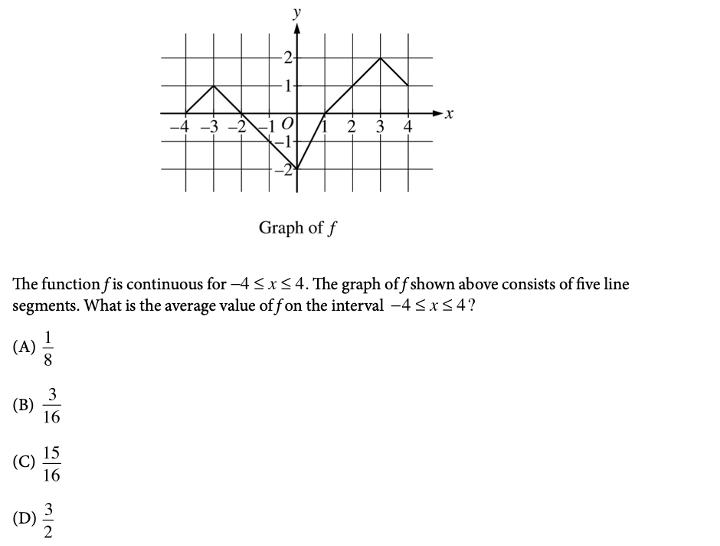
\(\frac{1}{2}(3)(-2)=-3\)
Question 5


Question 6
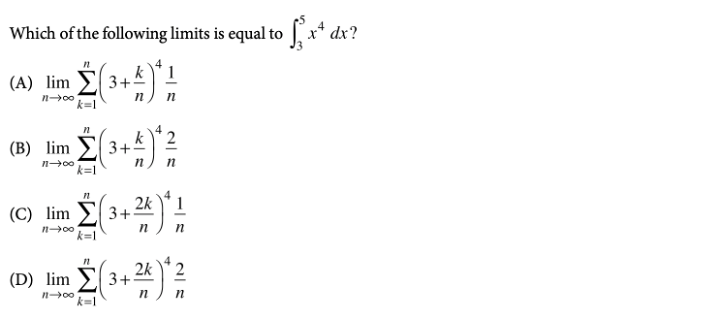
Question 7

Question 8

Question 9

Question 10

Final Tips
Know your calculator!
Time yourself

