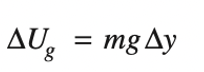10 Hardest AP Physics 1 Questions
What’s Covered
- How Will AP Scores Impact Your College Chances?
- Overview of the AP Physics 1 Exam
- AP Physics 1 Practice Questions
- Final Tips
With only 7% of test-takers receiving a 5, and only 42% of students passing in 2021, the AP Physics 1 Exam is notoriously difficult. Whether it’s the tricky concepts or tough calculations, this exam will require you to have a strong command of physics. In this post, we’ll cover some of the more difficult problems that you may encounter, along with solutions and test-taking strategies to best prepare you for the AP Physics 1 Exam.
How Will AP Scores Impact My College Chances?
Short answer: they don’t!
While AP scores don’t directly affect your college chances, you should still take the exams. Passing the exams might mean receiving college credit, depending on which school you end up attending.
Rather than looking at your AP exam scores, colleges instead look at the AP classes themselves. Colleges want to see that you’re challenging yourself by taking the most difficult courses available at your high school. To see how your course rigor stacks up against other applicants, check out CollegeVine’s free Admissions Calculator! This tool will take into account your courses, GPA, test scores, and more to determine your unique chances at your prospective schools.
Overview of the AP Physics 1 Exam
The AP Physics 1 Exam consists of the following sections:
Section I: Multiple Choice
- 50 multiple choice questions (1 hour, 30 minutes), 50% of exam score
Section II: Free Response
- 5 free-response questions (1 hour, 30 minutes), 50% of exam score
The multiple-choice section consists of both independent questions and questions associated with a stimulus or data set. Also, there will be 5 individual multi-select questions in which you’ll need to pick two answer choices.
In the free-response section, the questions are broken down into the following types:
- Experimental Design (1 question)
- Qualitative/Quantitative Translation (1 question)
- Short Answer: Paragraph Argument (1 question)
- Short Answer (2 questions)
You’ll be allowed a scientific or graphing calculator throughout the entire exam, and you’ll also be given equation and formula tables.
10 Hardest AP Physics 1 Questions
Question 1
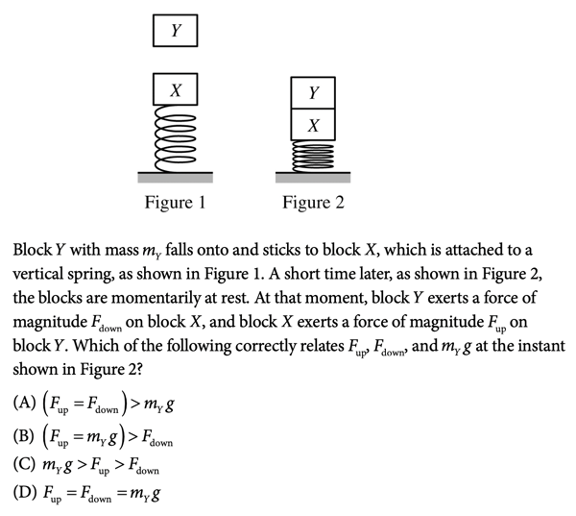
Answer: A
First, we’ll need to rely on Newton’s Third Law of Motion. This law states that two bodies exert forces of equal magnitude and opposite direction on each other. In this case, the force that block Y exerts on block X has magnitude \(F_{down}\), and the force that block X exerts on block Y has magnitude \(F_{up}\). By Newton’s Third Law, these forces should be equal in magnitude. So, we have that \(F_{down} = F_{up}\).
Next, to compare these two forces to \(m_{Y}g\), we’ll need to take a close look at the forces acting on block Y. If we were to draw a force diagram of these blocks, it would look like this:
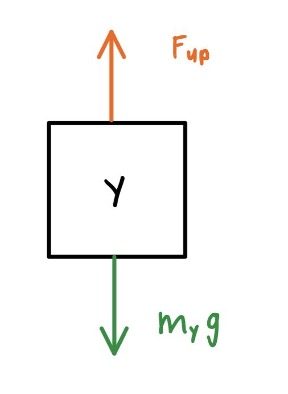
We see that the gravitational force of magnitude \(m_{Y}g\) acts downwards on block Y. Also, the force of block X on block Y with magnitude \(F_{up}\) acts upwards on block Y. To compare the magnitudes of these two forces, we need to determine the direction of the acceleration (this is because \(F_{net}\), the net force, will have the same direction).
Because block Y was initially moving downwards, then slowed down to a stop, we know that the acceleration is in the opposite direction of motion. So, the acceleration is in the upwards direction. Then, because \(F_{up}\) is in the same direction as acceleration and \(m_{Y}g\) is in the opposite direction of acceleration, we have that \(F_{net}=F_{up}-m_{Y}g\).
Then, \(F_{up}=F_{net}+m_{Y}g\).
So, we must have that \(F_{up} \gt m_{Y}g\).
Then, the correct answer is \((F_{up}=F_{down}) \gt m_{Y}g\).
Question 2
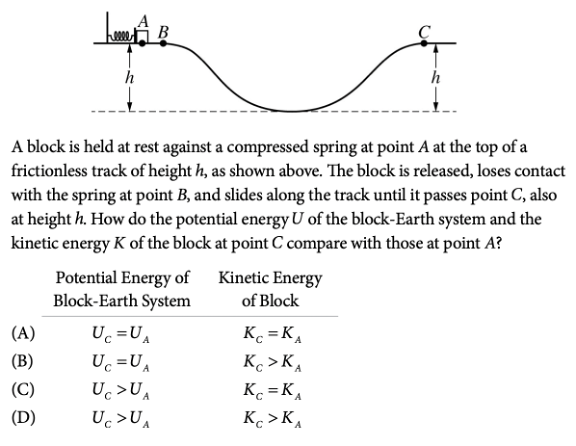
Answer: B
We can first analyze the potential energy of the block-Earth system at points A and C. We have the following formula:
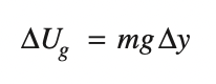
In this equation, \(U_g\) is the change in gravitational potential energy, \(m\) is the mass, \(g\) is the gravitational constant (\(9.8\ m/s^2\)), and \(\Delta y\) is the change in height.
So, the gravitational potential energy at point A is: \(U_{A}=mgh\).
And, the gravitational potential energy at point C is: \(U_{C}=mgh\).
So, \(U_{A}=U_{C}\). This makes sense because the block is at the same height at points A and C, so the potential energy of the block-Earth system (which is dependent on height) is the same.
Next, let’s look at the kinetic energy by analyzing the total energy. We can assume that the total energy of the system is conserved since the track is frictionless.
So, the total energy at point A is equal to the total energy at point C. Next, let’s consider what types of energy we have at each point. We know that we have to consider gravitational potential energy and kinetic energy at each point. But, we also have to look at the potential energy given by the spring at point A.
Point A: \((Total\ Energy)_{A}=U_{A}+K_{A}+U_{S}\), where \(U_S\) is the potential energy given by the spring.
Point C: \((Total\ Energy)_{C}=U_{C}+K_{C}\). Since there is no spring force acting on the block at point C, we don’t have to consider spring potential energy at point C.
Since these total energies should be equal to each other we have:
\(U_{A}+K_{A}+U_{S}=U_{C}+K_{C}\)
Then, \(K_{A}+U_{S}=K_{C}\) (because \(U_{A}=U_{C}\)). So, we can clearly see that \(K_{A}\lt K_{C}\), and the correct answer choice is B.
Question 3
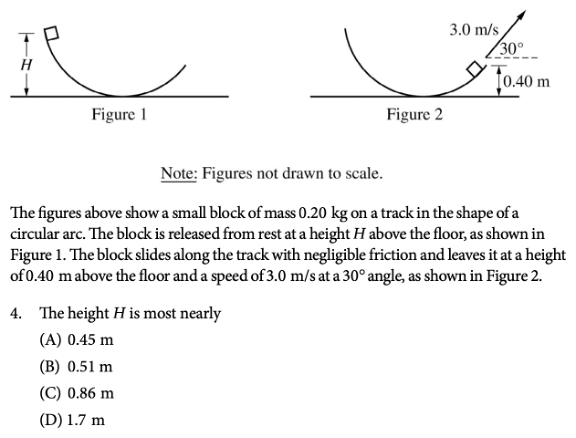
Answer: C
To answer this question, we can once again analyze the energy at both points. Since friction is negligible, we know that the total energy at both points is conserved, and therefore equal.
So, the total energy at the beginning of the track consists only of gravitational potential energy. The total energy at the end of the track consists of both gravitational potential energy and kinetic energy.
So, \(U_{initial}=U_{final}+K\), where \(U\) is potential energy and \(K\) is kinetic energy.
We’ll use the following formulas:
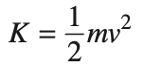
In the second equation, \(K\) is the kinetic energy, \(m\) is the mass, and \(v\) is the speed.
We see that \(U_{initial}=mgH\), since the block is initially at height \(H\).
Also, \(U_{final}=mg(0.4)\), since the block is at height \(0.40\ m\) at the end of the ramp.
Finally, \(K=\frac{1}{2}mv^2\).
Then, our original equation becomes \(mgH=mg(0.4)+\frac{1}{2}mv^{2}\).
We can cancel out \(m\) from each term to get: \(gH=g(0.4)+\frac{1}{2}v^{2}\).
Let’s solve for \(H\):
\(H = \frac{[g(0.4)+\frac{1}{2}v^2]}{g}\).
Filling in \(g = 9.8 m/s^2\) and \(v = 3.0 m/s\), we get: \(H = \frac{[9.8(0.4)+\frac{1}{2}(3)^2]}{9.8}\).
Once we solve for \(H\), we see that \(H=0.86\ m\).
Question 4

Answer: B
For this question, we’ll need to rely on the following formula:
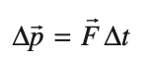
In this equation, \(\Delta p\) is the momentum, \(F\) is the force, and \(\Delta t\) is the change in time.
So, if we compute the area under the curve for each object, we’ll be able to determine the change in momentum for each. Since the areas under both curves have the shape of a triangle, we can simply use the triangle area formula to compute momentum.
Object X: \(\Delta p_{x}=\frac{1}{2}(F_0)(t_0)\)
Object Y: \(\Delta p_{y}=\frac{1}{2}(2F_0)(\frac{t_0}{2})=\frac{1}{2}(F_0)(t_0)\)
Then, we see that \(\Delta p_{x}=\Delta p_{y}\).
Question 5
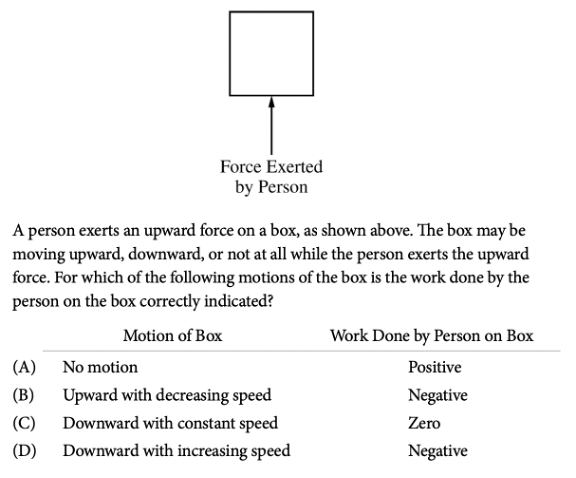
Answer: D
We’ll first need to recall the equation for work:

Note that the force which contributes to work (\(W\)) is the force (\(F\)) that acts parallel to the direction (\(d\)) of motion.
In this case, since the force is exerted upwards, we have that the work done by the person is positive if the motion is upwards and negative if the motion is downwards.
So, the correct answer choice is D. Notice that answer choice C is incorrect since even if the box is moving at a constant speed, the person does negative work on the box because the applied force is opposite the direction of motion.
Question 6

Answer: A
This problem is tricky in that we’ll need to work with equations involving unknowns since we’re not really given many concrete numbers. So, our strategy will be to analyze the equations in terms of the unknowns in order to compare them.
Let’s first look at the relevant equations for gravitational force and circular motion:
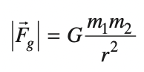
In this equation, \(F_g\) is the gravitational force, \(G\) is the gravitational constant, \(m_1\) is the mass of the first object, \(m_2\) is the mass of the second object, and \(r\) is the radius, or distance between the two objects.
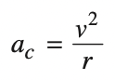
In this equation, \(a_c\) is the centripetal acceleration, \(v\) is the speed, and \(r\) is the radius.
We can first solve for the gravitational force on each satellite, using the first equation:
\(F_{1} = G \frac{m_{0} m_{E}}{(2R_{E})^2}=\frac{1}{4}(G\frac{m_{0} m_{E}}{(R_{E})^2})\)
\(F_{2} = G \frac{2m_{0} m_{E}}{(3R_{E})^2}=\frac{2}{9}(G\frac{m_{0} m_{E}}{(R_{E})^2})\)
Since \(\frac{1}{4} \gt \frac{2}{9}\), we see that \(F_{1} \gt F_{2}\).
Next, we’ll need to use the second equation to compute the speed of each satellite. In this case, the centripetal force is caused by the gravitational force, so we have that \(F_{c} = F_{g}\) for each satellite.
Then, because \(F_{c}=m_{0}a_{c}\), we can solve for the centripetal acceleration for each satellite using the equation \(a_{c}=\frac{F_{c}}{m_{0}}=\frac{F_{g}}{m_{0}}\).
\(a_{c1}=\frac{1}{4}(G \frac{m_E}{(R_E)^2})\)
\(a_{c2}=\frac{2}{9}(G \frac{m_E}{(R_E)^2})\)
Because \(a_{c}=\frac{v^2}{r}\), we see that:
\(a_{c1}=\frac{1}{4}(G \frac{m_E}{(R_E)^2}) = \frac{(v_1)^2}{2R_E}\)
\(a_{c2}=\frac{2}{9}(G \frac{m_E}{(R_E)^2}) = \frac{(v_1)^2}{3R_E}\)
Solving for the speed, we get:
\((v_1)^2 = \frac{1}{2} (G\frac{m_E}{R_E})\)
\((v_2)^2 = \frac{1}{3} (G\frac{m_E}{R_E})\)
Then, we see that \(v_1 \gt v_2\).
Question 7
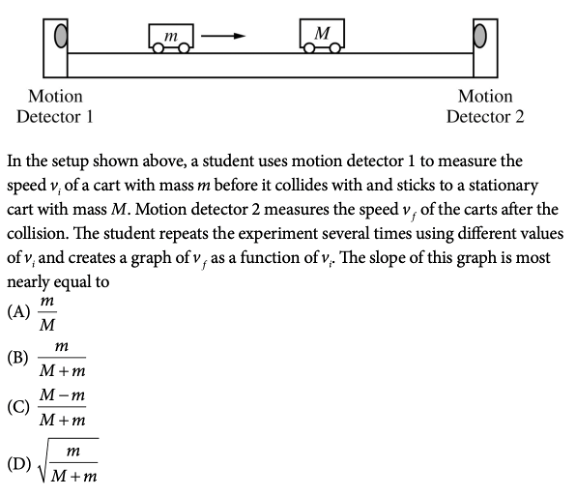
Answer: B
This question wants us to analyze the momentum of the two carts. Because momentum is conserved, we can analyze the momentum before and after the collision and set it equal to each other.
The given equation for momentum is as follows:
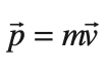
In this equation, \(p\) is the momentum, \(m\) is the mass, and \( v\) is the velocity.
Before the collision, because only the left is moving, we have that: \(P_i = mv_i\)
After the collision, since both carts are moving together at the same speed, we have that: \(P_f = (m+M)v_f\).
Since \(P_i=P_f\), we have that \(mv_i=(m+M)v_f\).
Next, the student wants to create a graph of \(v_f\) as a function of \(v_i\). So, let’s solve for \(v_f\) to determine the slope of the line:
\(v_f = (\frac{m}{m+M})v_i\)
So, we see that the slope is \(\frac{m}{m+M}\).
Question 8
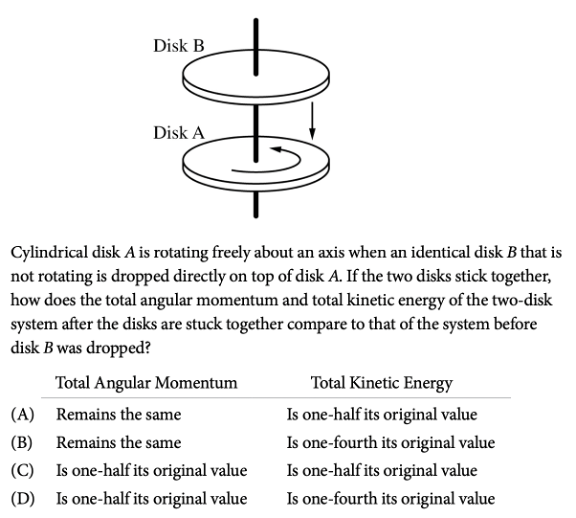
Answer: A
When discussing angular momentum, we should recall that angular momentum is always conserved.
So, the total angular momentum before and after the collision should be the same. This means that the correct answer choice is either A or B.
Also, let’s use this fact to set up equations in order to learn more about the system. The equations that we’ll use are:

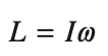
In the second equation, \(L\) is the angular momentum, \(I\) is the moment of inertia, and \(\omega\) is the angular velocity.
Because momentum is conserved, the momentums before and after are equivalent.
Before:
Momentum: \(p_i = mv_i\)
Angular momentum: \(L_i=I\omega _i\)
After:
Momentum: \(p_f = 2mv_f\)
Angular momentum: \(L_f = 2I \omega _{f}\)
Because disks A and B are identical, they have the same mass and moment of inertia, so after the collision, we have double the mass and double the moment of inertia.
Using \(p_i=p_f\) and \(L_i=L_f\) , we can solve for \(v_f\) and \(\omega _f\) to get that:
\(v_f = \frac{1}{2} v_i\)
\(\omega _f = \frac{1}{2} \omega _i\)
Now, we can use this information to analyze the total kinetic energy of the system. Let’s use the following equations:

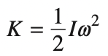
The first equation is for translational kinetic energy and the second equation is for rotational kinetic energy, and we’ll need to consider both to compute the total kinetic energy.
The total kinetic energy before the collision is:
\(K_i = \frac{1}{2} mv_i \ ^2 + \frac{1}{2} I\omega _i \ ^2\)
Then, the total kinetic energy after the collision is:
\(K_f = \frac{1}{2} (2m)v_f \ ^2 + \frac{1}{2} (2I)\omega _f \ ^2\)
\(= mv_f \ ^2 + I\omega _f \ ^2\)
\(= m(\frac{1}{2} v_i)^2 + I(\frac{1}{2} \omega _i)^2\)
\(= \frac{1}{2}(\frac{1}{2} mv_i \ ^2 + \frac{1}{2} I\omega _i \ ^2)\)
\(= \frac{1}{2} K_i\)
So, the kinetic energy is one-half its original value.
Question 9

Answer: B, D
This question is one of the infamous multiple-select questions, so you’ll need to be extra careful when selecting your answers. Let’s go through each answer choice and determine whether it’s true or not.
For answer choice A, we’ll need to note that the satellite’s rotational kinetic energy is dependent on the radius. But, since the orbit is elliptical, the radius is changing. Then, the kinetic energy is not constant, so this statement is false.
For answer choice B, we need to recall that in elliptical orbit motion, angular momentum is always constant, so this statement is true.
For answer choice C, recall that linear momentum is dependent on mass and velocity. Though the mass is constant, the velocity is constantly changing since the satellite is moving in an ellipse (which means the radius is changing and thus so is velocity). This means that the linear momentum is not constant and this statement is false.
Finally, for answer choice D, we’ll need the following equation:
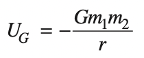
In this equation, \(U_G\) is the gravitational potential energy.
So, this quantity is the largest when \(r\) is the largest, which means the statement is true.
Question 10

Solution:
Student 1 claims that the sphere can’t move in a circle because none of the forces acting on it are in the direction of point C. But, what the student is forgetting is that the centripetal force is a net force, which means it’s the accumulation of all forces acting on the object. So, even though none of the individual forces are pointing in the direction of point C, their sum could be pointing in that direction. Also, the tension force exerted by the string on the sphere has a horizontal component in the direction of C which contributes to the centripetal force.
Student 2 claims that the tension force exerted by the string is less than the weight of the sphere because of the angle, which means it should be moving downwards. But, what the student doesn’t realize is that the magnitude of the tension forces and the weight are not necessarily equal. So, the magnitude of the tension force could be large enough that the vertical component of it is still larger than or equal to the weight (even with the angle).
Final Tips
Learn to effectively use your calculator
To do well on the AP Physics 1 Exam, you’ll need to make good use of your calculator. So, to maximize your chances of success, you should make sure that you’re comfortable using your calculator. This means knowing how to use your calculator as efficiently as possible. Instead of relying on it as a crutch, your calculator should be a supplement to help you solve questions more quickly.
To avoid careless errors or rounding mistakes, it’s best to plug into your calculator at the last possible second. So, try to write out each step carefully and avoid computing until your final step. This way, you can minimize both the amount of time you spend using the calculator and the chances of making a careless mistake.
Review the formula sheet
Because you’re provided with a formula sheet, you should be sure that you’re familiar with it prior to taking the exam. As you take practice exams or complete practice problems, make sure to use the given AP formula sheet. This way, you’ll be more comfortable with the layout of the formulas, and you’ll be able to quickly locate relevant formulas on the day of the exam. Because the formula sheet is so lengthy, it’s important that you take time to review it before test day.
Make up your own practice problems
Once you’ve exhausted the official practice problems, it can be helpful to make up your own. Pinpoint which types of problems you struggled with the most, then adjust the numbers and try to solve it again. This way, you’ll familiarize with yourself the format of the solutions as you practice.
Also, try completing similar problems, but with a different unknown. For example, if you’re struggling with a kinematics problem in which you’re given velocity and time and are asked to solve for acceleration, try creating another problem in which you’re given acceleration and velocity, but are asked to find time. This way, you’ll become even more comfortable solving different kinds of problems covering the concepts that you’re struggling with.
Check out some of CollegeVine’s other helpful guides: