SAT Math Probability Practice Questions

What’s Covered:

• Overview of the SAT Math Test
• Important SAT Probability Concepts + Practice Questions
• How Will My SAT Score Impact My College Chances?

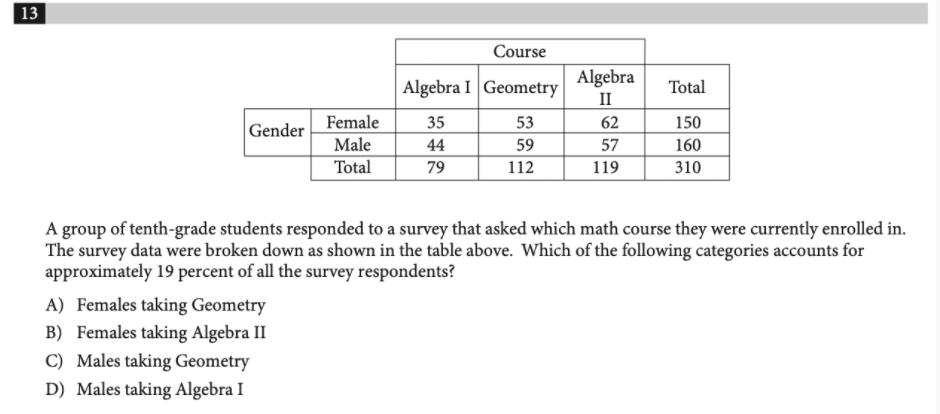
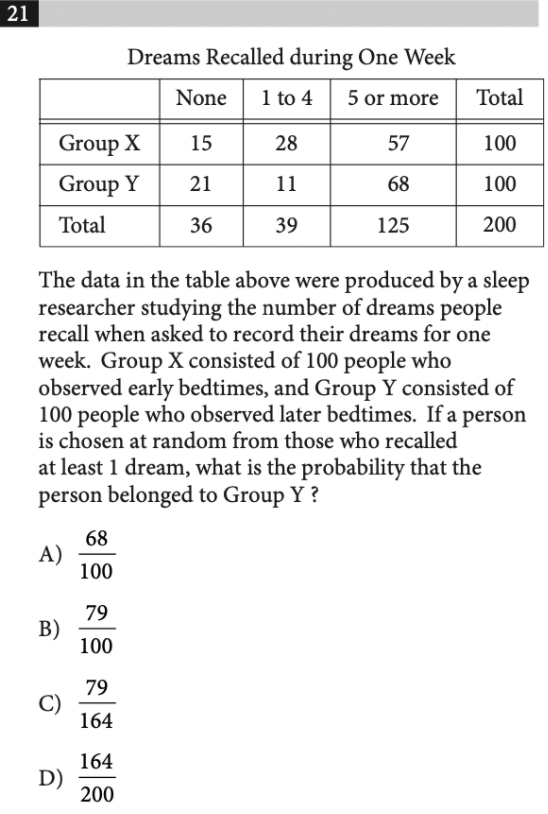
What are your chances of acing the SAT Math Test? Well, if you’ve mastered the mathematical concepts that you’ll be tested on, you’ll likely get a competitive score. One of these important concepts is probability– on most SAT Math Tests, you’ll find at least one probability question. With sufficient practice, these questions will mean easy points! In this article, we’ll cover important strategies for solving probability questions on the SAT Math Test.

Overview of the SAT Math Test

The SAT Math Test consists of two sections, the No calculator section and the Calculator section. In total, you will be asked to answer 58 questions in 80 minutes. The questions are sorted into the following categories:

• Heart of Algebra
• Problem Solving and Data Analysis
• Passport to Advanced Math
• Additional Topics in Math

Probability questions fall into the second category, Problem Solving and Data Analysis. You’re more likely to find questions involving probability on the Calculator section of the SAT Math Test. More often than not, these questions will show up in the form of a table. It’s important to read carefully and know what the question is asking for to be able to correctly answer it. Once you get the hang of it, these types of questions will start to become no-brainers!

Important SAT Probability Concepts + Practice Questions

All of the following practice questions are taken from official SAT practice tests. 

Proportions

Knowing how to compute proportions is a necessary skill when it comes to probability. In fact, many probability questions are essentially proportions in disguise. To set up a correct proportion, you can follow this general rule of thumb:

\(Proportion=\frac{What\:you\:want}{What\:you’re\:looking\:for}\)

This means that, when you set up your fraction, you want the population of interest in the numerator, and the total population considered in the denominator. Let’s contextualize this with a concrete example:

Answer: B

This question is asking for the proportion of adults who received a sugar pill that reported contracting a cold.

So, our population of interest is adults who received a sugar pill and reported contracting a cold. But, we’re looking at all adults who received a sugar pill.

Then, our fraction is: \(\frac{Adults\:who\:received\:a\:sugar\:pill\:and\:contracted\:a\:cold}{Adults\:who\:received\:a\:sugar\:pill}\)  

Now, we can look at the table to find the exact numbers. The total number of adults who received a sugar pill is 150, and the number of adults who received the sugar pill and contracted a cold is 33.

So, our proportion is 33/150, or 11/50.

Here’s a less straightforward question involving proportions:

Answer: C

This time, we’re given a proportion (19%) and are asked to work backward to find the population of interest. We see that the question says “19 percent of all survey respondents,” so this means that the total population we’re looking at is all survey respondents, which is 310 people.

If we set up our proportion, we get \(\frac{x}{310}=.19\), where \(x\) represents the population of interest. If we solve for \(x\) (remember, a calculator is allowed for this question), we get that \(x=58.9\) which is approximately \(59\).

Let’s look at the table to see that \(59\) corresponds to males taking geometry, so answer choice C is correct.

Single-event probability

These types of questions are the most common probability questions on the SAT Math Test. Luckily, solving these questions is a lot like solving ones involving proportions, so we can apply that same logic.

We denote the probability of an event, \(E\), as \(P(E)\). This reads as “the probability of E.”

Let’s jump straight into an example:

Answer: D

This question asks us for the probability that a gas station customer did not purchase gasoline. Let the event that a customer did not purchase gasoline be denoted by \(N\).

So, \(P(N)=\frac{number\:of\:customers\:who\:did\:not\:purchase\:gasoline}{total\:number\:of\:customers}=\frac{50}{135}\), which corresponds to answer choice D.

As you can see, probability problems typically involve the use of proportions.

“Or” 

Another keyword in probability is the word “or.” This is also called the union of two events. Essentially, if we have two events, \(A\) and \(B\), the probability of \(A\) or \(B\) can be given by the following formula.

\(P(A\:or\:B)=P(A)+P(B)-P(A\:and\:B)\)

Again, this makes more sense within the context of a sample problem:

Answer: B

Let’s begin by naming our events. Let the event that the winner is a female under age 40 be denoted by \(F\), and let the event that the winner is a male age 40 or older be \(M\).

Then, \(P(5)=\frac{8}{25}\) (this is because there are 8 females under 40, and we’re looking at all those who entered the contest, a total of 25 individuals). Similarly, \(P(M)=\frac{2}{25}\).

Next, we’ll need to find the \(P(F\:and\:M)\). This probability is actually \(0\) because according to the table, there are no individuals who are both a female under 40 and a male 40 or older.

Then, \(P(F\:or\:M)=P(F)+P(M)-P(F\:and\:M)=\frac{8}{25} + \frac{2}{25} – 0=\frac{10}{25}\).

“Given” 

Like “or,” “given” is an important word within the context of probability. We use the symbol \(P(A|B)\), which reads as “the probability of event \(A\), given event \(B\).” The formula for this is as follows:

\(P(A|B)=\frac{P(A\:and\:B)}{P(B)}\)

This formula isn’t given on the SAT, but if you have it memorized and handy, it makes these types of questions a lot easier to answer without making careless mistakes.

Here’s an example where using the formula will help us:

Answer: C

Again, let’s denote our events. Let \(A\) be the event that a tablet user answered “Always,” and let \(B\) be the event that the tablet user did not answer “Never.” Then, the question is asking us to find \(P(A|B)\).

According to our formula, we’ll need to know \(P(A\:and\:B)\) and \(P(B)\). Let’s start with \(P(B)\). According to the table, the percent of those who did not answer “Never” is \(24.3+13.5+30.9=68.7%\).

To find \(P(A\:and\:B)\), we’ll need to think about the individuals who answered “Always” and did not answer “Never.” This population actually includes all those who answered “Always” (since if they answered “Always,” they did not answer “Never”). So, \(P(A\:and\:B)=P(A)=30.9%\).

Now, we have everything we need to solve the problem:

\(P(A|B)=\frac{P(A\:and\:B)}{P(B)}=\frac{30.9}{68.7}\) is approximately \(0.45\).

More probability practice!

Let’s put your skills to the test with some problems which are on the trickier side.

Answer: C

Let’s look at the last sentence to figure out what the question is asking. We want the probability that a person is chosen from those who recalled at least 1 dream is in Group \(Y\).

So, the population of interest is those who recalled at least 1 dream and are in Group \(Y\), and the total population that we’re looking at is all those who recalled at least 1 dream:

\(P=\frac{Recalled\:at\:least\:1\:dream\:and\:in\:Group\:Y}{Recalled\:at\:least\:1\:dream}\)

From the table, the total number of people in Group Y who recalled at least 1 dream is \(11+68=79\), since we need to look at the groups “1 to 4” and “5 or more.” Also, the total number of people who recalled at least one dream is \(39+125=164\).

So, our probability is \(\frac{79}{164}\), which corresponds to choice C.

Answer: 8

This problem asks us to work backward. We are given a probability of 1/9, but we need to figure out what this probability means. The question states that this is the probability of a person having blood type B, given that they were chosen from the group of people who are rhesus negative (-).

So, if we let \(B\) denote the event that a person has blood type B and let \(N\) denote the event that a person is rhesus negative, we have that \(P(B|N)=\frac{1}{9}\).

Using the formula from earlier, this means that \(P(B|N)=\frac{P(B\:and\:N)}{P(N)}\).  From the table, we know that \(P(B\:and\:N)\) is 2, and \(P(N)=7+2+1+x\), so we have the following equation with which we can solve for \(x\):

\(\frac{2}{7+2+1+x}=\frac{1}{9}\)

\(\frac{2}{10+x}=\frac{1}{9}\)

Now, we can cross multiply to get:

\(2(9)=10+x\)

\(18=10+x\)

\(x=8\).

How Will My SAT Score Impact My College Chances?

Though many colleges have become test-optional in the past and current admissions cycles, the SAT score has been used as a predictor of an applicant’s future collegiate success. Schools use your standardized test scores (in conjunction with your GPA) to determine your level of academic achievement, a hefty factor in the college admissions process.

Having strong test scores is a great way to maximize your chances of success. To see how your score affects your chances, check out CollegeVine’s free Admissions Chances Calculator. This calculator will take into account your GPA, test scores, extracurriculars, and more to give you a personalized estimate of your chances at the schools of your choice!

Other posts you may like:

• 30 SAT Math Formulas You Need to Know
• 15 Hardest SAT Math Questions