10 Hardest PSAT Math Questions
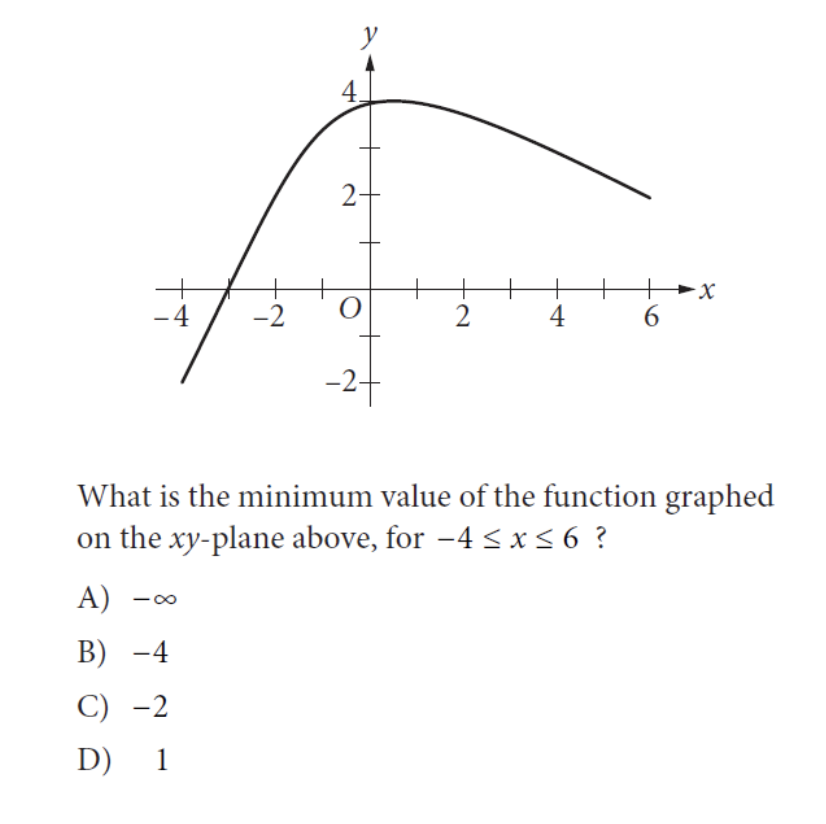
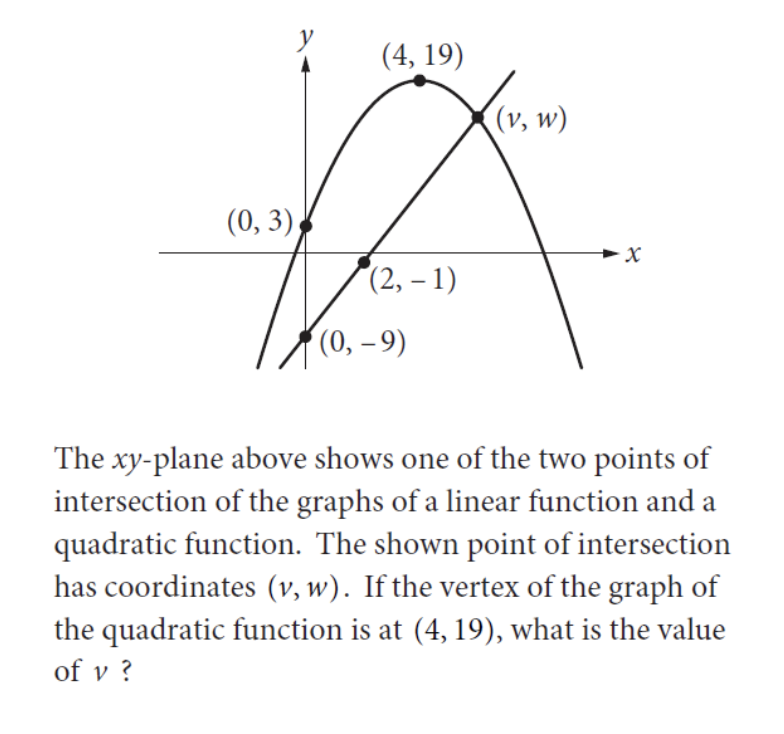
The PSAT is much more than a practice exam. While your performance on the PSAT will certainly help you prepare for the SAT by indicating which areas you need to improve upon, it can also make you eligible for national scholarships! The Math Section of the PSAT tests student’s on various mathematical concepts, both with and without a calculator. Keep reading as we breakdown and explain some of the most difficult PSAT Math practice questions to prepare you for test day! The Preliminary SAT/National Merit Scholarship Qualifying Test (PSAT/NMSQT), normally taken by high school juniors and sophomores, measures what you’ve learned in school and opens up doors for scholarship opportunities as well as the National Merit Scholarship Program. The exam is typically three hours long and is divided into two sections: Evidence-Based Reading & Writing (which is further divided into the Reading Test and Writing Test), and the Math Section (which is divided into the Calculator and No Calculator portions). Unlike the SAT, the PSAT has an overall score of 1520, with the scores for each section ranging from 160-760. As mentioned earlier, there are two separate portions of the Math Test: Calculator and No Calculator. The Math Test deeply focuses on three different areas of math, which include mastery of linear equations and systems, problem solving and data analysis, and the manipulation of complex equations. In addition to these main concepts, geometry and trigonometry concepts that are relevant to college are also tested. 83% of the Math Test is multiple choice questions, while 17% of the Math Test is grid-in questions, in which students are expected to enter their answers in the grids provided on the answer sheet. The PSAT is an optional exam that does not have an impact on your chances of getting into college. However, since the PSAT is very similar to the actual SAT in terms of scoring, format and content, being prepared for the PSAT can make you equally prepared for the SAT. Furthermore, your PSAT score can give you a good understanding of how to prepare for the SAT. The PSAT is also used as a qualifying exam for the National Merit Scholarship, which awards different levels of recognition based on the PSAT score you receive. These titles include Commended Students and Semifinalists. If you are selected as a Semifinalist, you can apply to compete in the National Merit Scholarship Program. If your application is outstanding, you may be chosen to be a Finalist. As a finalist, you earn the title of National Merit Scholarship recipient and can be awarded National Merit Scholarships to help fund your college tuition. For more information on how your PSAT score can impact your college chances, feel free to use our free chancing engine. This tool will calculate your odds of acceptance at hundreds of schools across the country based on your tests scores, GPA, extracurriculars, and more. The Math test, as mentioned below, tests on a multitude of topics taught over the course of high school. The PSAT is meant to test how well you are able to apply the math skills and knowledge you’ve learned. While the difficulty of questions asked on the PSAT Math section range from easy to hard, in this post, we show you how to break down and solve 10 of the hardest PSAT math questions. Correct Answer: (A) This is a math question that requires you to understand how percentages work. In this question, both the production of tomatoes and raspberries decrease by a percentage. In order to find the percentage by which the total yield of Boyd’s garden declined, we need to find out how many tomatoes and raspberries were lost in production. Since the total amount of tomatoes declined by 20%, we know that the tomatoes declined in production by 0.20 × 140 = 28 pounds. Meanwhile, the raspberries declined in production by 0.5 × 60 = 30 pounds. The percent decline in the total yield can be found by dividing the decline in number of pounds of tomatoes and raspberries by the previous year’s production: (28 + 30) / (140 + 60) = 29% it is important to realize that the question is asking for the decline of the total yield. If the question were asking for the percentage of the garden that was retained this year, the calculation would be different. In this case, we would calculate the total tomatoes and raspberries produced this year (instead of the production that was lost) and divide that by the total production of last year (which would be 71%). Correct Answer: (C) This question is quite tricky because, at first glance, it seems as if there is no minimum to the graph, only a maximum. So the initial reaction might be to assume that the minimum value of the function is negative infinity. However, when reading carefully, the question asks for the minimum of the graph in the restricted domain of x between -4 and -6, inclusive. Therefore, the minimum value of the function occurs at the point (-4, -2), thereby making -2 the minimum value of the function. Correct Answer: (B) This question requires us to both analyze data and utilize percentages as well as ratios to come to our solution – so there are quite a few steps in this problem! First, we realize that there are a total of 61 + 48 = 109 students enrolled in the Propel program. Now, we know that the ratio of boys to girls is 2:3. This may seem like we can immediately multiply 109 by ⅔ to determine how many girls are in the program. However, we need to realize that a ratio of 2:3 implies that there are two boys and three girls for every group of 5 students. Therefore, we multiply 109 by ⅗ to determine how many girls are in the program, which is roughly 65 girls. Correct Answer: (C) This problem combines both geometry and systems of equations together in one problem. Let us assume that S is the length of each side of the square sculpture while T is the length of each side of the equilateral triangle sculpture (both in inches). Since both sculptures are made of a rod of the same length we know that the perimeter of each shape is the same. The perimeter of the square sculpture is 4S while the perimeter of the triangle sculpture is 3T: 4S = 3T We also know that each side of the triangle is 2 inches longer than each side of the square. This means that S + 2 = T. If we substitute the following equation in for the one we found above, we get: 4S = 3(S + 2) 4S = 3S + 6 S = 6 If the length of the side of the square sculpture is equal to 6 inches, that means the rod is 4 × 6 = 24 inches in length. Correct Answer: 6 One concept in math you should become very familiar with is graphs and their respective equations. The equation for a parabola is y = a(x-b)² + c where b is the x coordinate of the vertex, c is the y coordinate of the vertex, and a is a coefficient that can be found from the equation. Since we know that the vertex of the graph is (4, 19), we can set up the parabola equation to be y = a(x-4)² + 19. Since we know that the parabola also passes through the point (0, 3), this means that a is equal to: 3 = a(0 – 4)² + 19 -16 = a(-4)² -16 = a(16) a = -1 Now that we know the equation of the parabola is y = -(x-4)² + 19, we can determine the equation of the linear function knowing that the function passes through the points (0, -9) and (2, -1). The slope of the function, which we know is equal to change in y-coordinates over change in x-coordinates of the line, is [(-1) – (-9)] / [2 – 0] = 4. Knowing that the y-intercept of the linear function is -9, we can write the equation of the linear function to be y = 4x – 9. With the two equations, we can now find the point at which the two graphs intersect through a set of equations. We can set the two equations equal to each other since both equations are solved for y: y = 4x – 9 (Linear equation) y = -(x-4)² + 19 (Parabola equation) 4x – 9 = -(x-4)² + 19 x² – 4x – 12 = 0 (x – 6) (x + 2) = 0 x = 6 and -2 Since (v,w) is on the positive side of the y-axis, v has to be equal to 6.
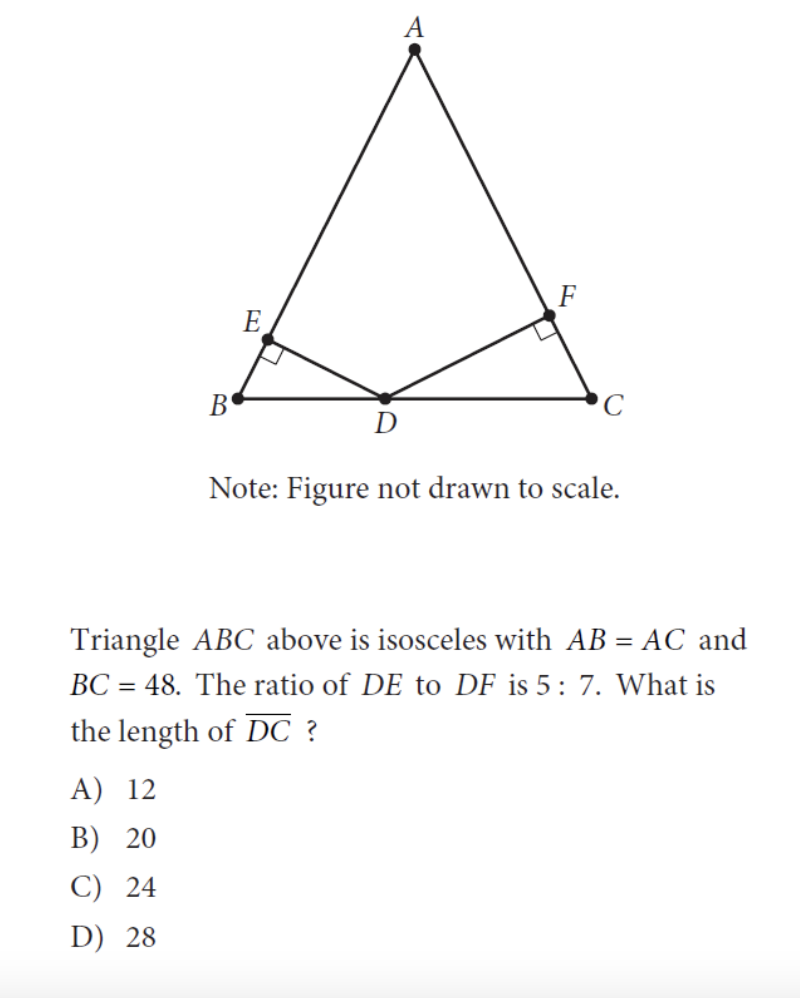
Correct Answer: 9 This is another system of equations question, however, this question is a bit more difficult since it is a word problem, so make sure to read the question carefully! Let’s say that x = number of sections studied by a group of two students, while y = number of sections studied by a group of four students. We know that there are 78 total students, which means that 2x + 4y = 78. We also know that there are 24 total sections, which means that x + y = 24. Now you can use either the substitution method or the elimination method to determine what x and y are equal to (review both of these methods since they will be extremely useful when taking the math portion of the PSAT)! Using the substitution method, we see that: 2x + 4y = 78 x + y = 24 → y = 24 – x 2x + 4(24 – x) = 78 2x + 96 – 4x = 78 -2x + 96 = 78 2x = 18 x = 9 Therefore, the total number of sections with two students is 9. Correct Answer: (D) This question is tricky since it requires you to remember how functions are written. We know that we are expected to solve the function for f(-3). Without initially reading the prompt, one may assume that x = -3 and incorrectly solve the problem. We see in the problem statement that the equation is written in terms of f(x – 1). Therefore, we need to determine the actual value of x: f(x – 1) = f(-3) = f(-2 – 1) Therefore, x = -2. Solving the equation for x = -2, we get: 2(-2) + 3 = -1 Correct Answer: 5 Another important skill to remember when studying for the math section of the PSAT is exponential rules, so make sure to review these! For this particular question, we need to remember the power rule as well as the product rule (as shown below): (x²y³)½ (x²y³)⅓ = xa/3ya/2 (x2 × ½ y3 × ½ )(x2 × ⅓ y3 × ⅓ ) = xa/3ya/2 (Power Rule) (xy3/2) (x2/3y) = xa/3ya/2 (xy3/2) (x2/3y) = xa/3ya/2 (x1 + 2/3y1 + 3/2) = xa/3ya/2 (Product Rule) (x5/3y5/2) = xa/3ya/2 (Simplification) From the simplified equation, we can see that a = 5 Correct Answer: (D) One additional topic tested on the PSAT is geometry and trigonometry. This means you should review equations related to shapes, geometry rules and basic trig! In this example, we see that we have to remember quite a few triangle rules to answer this question. In isosceles triangle ABC, we know that ∠B and ∠C are congruent (the same angle). Furthermore, ∠BED and ∠CFD are right angles which also makes them congruent. Since △BED and △CFD have angles that are corresponding, that means the two triangles are similar. A special rule of similar triangles is that all corresponding sides are proportional. Therefore, we know that BD/DC = DE/DF. Given that DE/DF = 5/7, we know that BD/DC = 5/7. With this given ratio, let’s write the following equation as a result of the proportionality: 5x = BD and 7x = DC. Other equations we know to be true from the problem statement are AB = AC and BC = 48. Knowing that BC = BD + DC, we know the following: BC = BD + DC = 48 5x + 7x = 48 12x = 48 x = 4 Therefore, the length of DC = 7x = 7(4) = 28 Correct Answer: 4 This question requires us to manipulate expressions through algebra. This question might seem hard at first sight since we are given a variable instead of a value to factor out – but don’t worry, we’ll review how to approach this problem! We know that x – 2 is a factor of the expression x² – bx + b. This means that x² – bx + b can also be written as (x – 2)(x – a) in which we need to solve for the value of a (notice that a is negative because the y-intercept of b is positive and two negative values make a positive). Expanding (x – 2)(x – a) = x² – 2x – ax +2a. Let’s now equate the two expressions we have and compare like terms to find the missing values: x² – 2x – ax +2a = x² – bx + b Compare like terms: -2x – ax = -bx → (cancel out the x) → -2 – a = -b 2a = b Since we know that 2a = b, we can substitute the value for b into our first equation to get: -2 – a = -(2a) -2 – a = -2a -2 = -a a = 2 Substituting a = 2 into 2a = b shows us that b = 4 Now that we’ve covered 10 of the hardest PSAT math questions, here are some final tips to remember when preparing for and taking the PSAT! As a high school sophomore or junior, preparing for the PSAT may seem like an additional stress you have to juggle in addition to AP/honors classes and extracurriculars. So remember, start early in terms of preparation and studying so that you will be more ready to take the PSAT in the fall! This way, you will be ready to take on the PSAT during the fall while still balancing the responsibilities school throws at you. The best way to prepare for the test is to practice, practice, practice! There are multiple ways to prepare for the PSAT. CollegeBoard has released a number of PDFs of previously administered PSATs online for free (as a note, the PSAT and PSAT 10 are essentially the same, however the PSAT 10 is not used to determine National Merit Scholarships). In addition, it is a good idea to review concepts of systems of equations, trigonometry, and algebra to prepare for the exam. Review concepts taught earlier in high school or even reach out to a math teacher to see if they have notes or prep material they can give to you. CollegeVine also offers numerous free, online PSAT resources that you might find helpful. Make sure that you read every question carefully. Oftentimes, CollegeBoard writes questions that are meant to stump you if you read the question too quickly. You might even accidentally find an answer to something they are not asking if you do so. So, take your time when reading the questions and make sure to double check your work with any time you have remaining! For more information about the PSAT, check out these articles:

What’s Covered:
Overview of PSAT
How Will My PSAT Score Affect My College Chances?
10 Hardest PSAT Math Questions
Question 1: Calculator, Multiple Choice
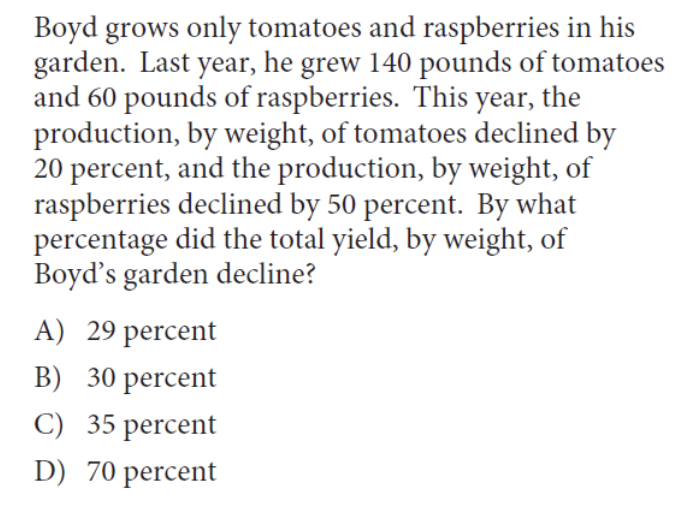
Question 2: Calculator, Multiple Choice
Question 3: Calculator, Multiple Choice

Question 4: Calculator, Multiple Choice

Question 5: Calculator, Grid In
Question 6: Calculator, Grid In

Question 7: No Calculator, Multiple Choice
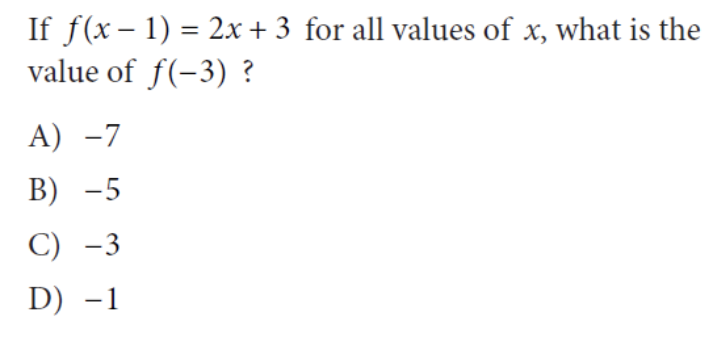
Question 8: No Calculator, Multiple Choice
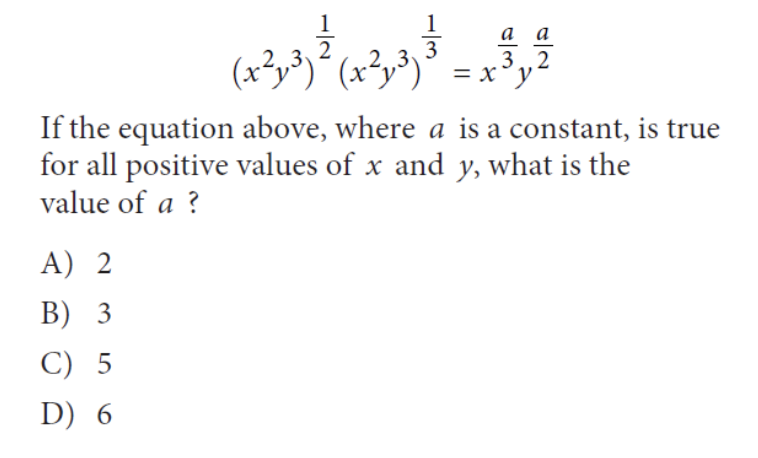
Question 9: No Calculator, Multiple Choice
Question 10: No Calculator, Grid In
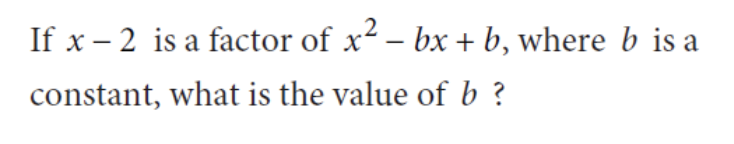
Final Tips
Start preparing early
Practice, Practice, Practice!
Read the questions carefully