AP Physics 1 Kinematics Equations You Need to Know + Practice Problems
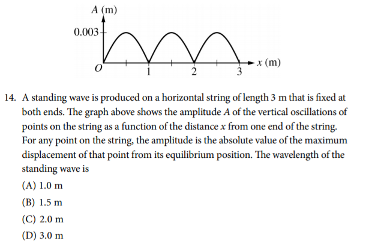
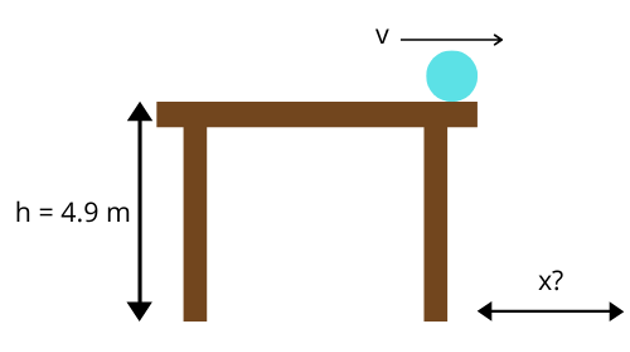
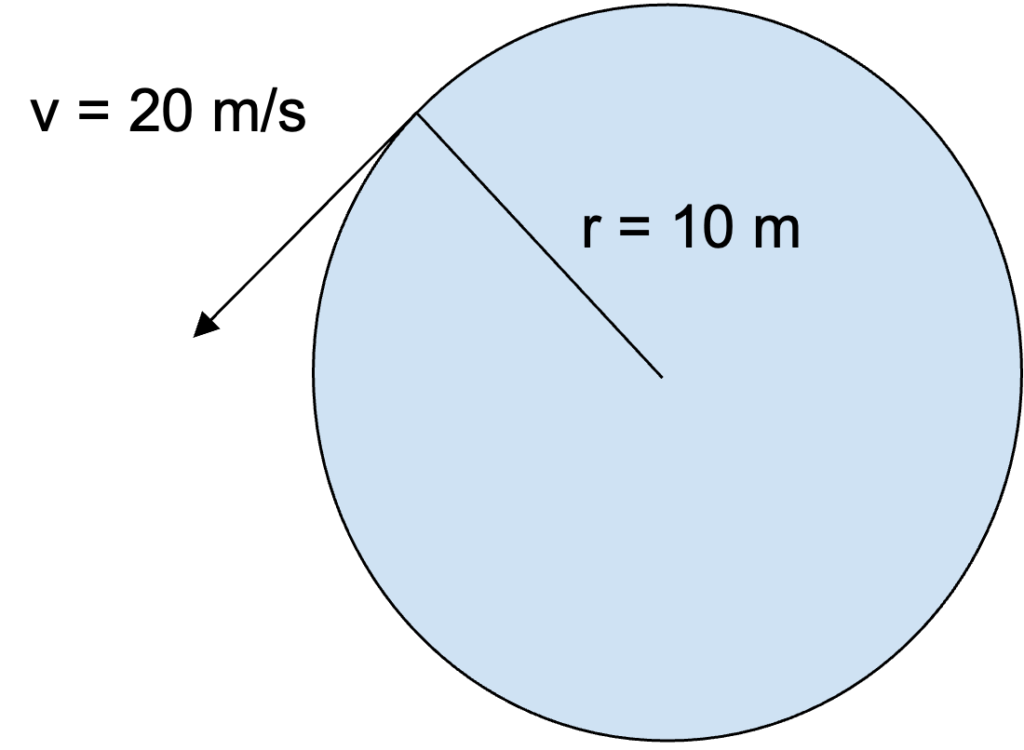
The AP Physics 1 exam requires you to think critically and analytically; you may need to use equations to find the amount of energy dissipated through a series of resistors, or create a detailed experimental procedure to determine the speed of sound in air at room temperature. In this article, we will review key AP Physics kinematics equations you’ll need to know to pass the AP Physics 1 Exam. We will cover these equations and then show you how you can use them in practice. The score you get on an AP exam, whether it be a 2 or a 5, will unlikely impact your chances of admission into a particular college. Colleges often will not review your scores, especially since you don’t have to self-report them if you don’t want to! College admissions will instead take a more holistic approach when reviewing your college application. Course rigor, GPA, essays, and extracurriculars are more likely to be valued when reviewing your application. When it comes to course rigor, colleges want to see how many APs you take and what grades you get in the classes rather than the exam scores (which are used to determine course credit and placement after you get into college). If you are interested in understanding how your course load impacts your chances at college, use our free chancing engine. This tool will help you determine your chances of acceptance at over 500 colleges based on your grades, test scores, extracurriculars and demographics. It is important to remember that when using this tool, your statistics are the only things being accounted for. Essays and letters of rec, which are not evaluated in this tool, are also important in the college acceptance process! The AP Physics 1 exam is an algebra-based, introductory college-level physics course. This class further prepares you for the AP Physics C course as well. The score you get on this exam helps determine which courses you may skip once you get into college. If you want to do well, you might want to check out the Ultimate Guide to the AP Physics 1 Exam since the article reviews tips and additional practice problems not covered in this article. The AP Physics 1 Exam is 3 hours long and consists of 50 multiple-choice questions and 5 free-response questions. Questions will cover everything taught in this course from mechanics to electricity. You will have 90 minutes to complete the multiple choice portion of the test. The multiple choice items are broken up into two different types of questions: 45 single-select multiple choice questions and 5 multiple-select multiple choice items. Single-select multiple choice questions are the ones we all know and love, such as the one shown below, in which there is one correct answer. Answer: C, Source: CollegeBoard Multiple-select multiple choice questions may require you to select one or more choices that could be the correct answer, as the one shown below. Answer: B, D, Source: CollegeBoard The Free Response Section, which lasts 90 minutes, consists of five questions that cover four different types of questions. The experimental design question assesses the test taker’s ability to design a scientific experiment. The qualitative/quantitative question requires you to be able to translate between quantitative and qualitative justification and reasoning. The paragraph argument short answer question assesses your ability to develop an argument about a physical phenomenon while the short answer question covers topics not asked in the other FRQs. All of these types of questions only show up once on the exam while the short answer question appears twice (1 experimental design + 1 qualitative/quantitative translation + 1 paragraph argument + 2 short answers = 5 FRQ questions). Both the multiple choice questions and free response questions are weighted at 50% to determine the final score. The AP Physics exam covers topics such as energy, momentum, DC circuits and Electrical Charge. The first thing you may learn in your AP Physics 1 course is kinematics. Kinematics deals with the motion of objects independent of the object’s mass and forces being applied to the object. Therefore, in this review, we will be exploring the relationships between acceleration, velocity, position and time. Note: The practice questions that appear are not official problems, but they will help you understand the concepts covered in this article. It is important to note that displacement, velocity, and acceleration are all vector quantities which means they indicate the direction the object is moving in. The following kinematics equations only apply to constant acceleration situations; this means that kinematics covers linear motion in one and two dimensions as well as circular motion. The following equations are applicable to linear and projectile motion: We are able to find the velocity at any given time if we know the initial velocity (\(v_{x0}\)) and acceleration (\(a_{x}\)). The position equation allows us to find the position at time \(t\) given that we know the initial velocity (\(v_{x0}\)), initial position (\(x_{0}\)) and acceleration (\(a_{x}\)). We may combine equations 1 and 2 to create a final kinematics equation that is independent of time. Rather, this equation combines initial velocity, current position, initial position and acceleration to find the velocity of the object at the current position. To derive this equation, we start with equation 1: From \(v_{x}=v_{x0}+a_{x}t\) we get: \(t=\frac{v_{x}-v_{x0}}{a_{x}}\) Substitute the found \(t\) into \(x=x_{0}+v_{x0}t+\frac{1}{2}a_{x}t^2\): \(x=x_{0}+v_{x0}(\frac{v_{x}-v_{x0}}{a_{x}})+\frac{1}{2}a_{x}(\frac{v_{x}-v_{x0}}{a_{x}})^2\) \(x=x_{0}+\frac{v_{x0}v_{x}}{a_{x}}-\frac{v_{x0}^2}{a_{x}}+\frac{1}{2}a_{x}(\frac{v_{x}^2-2v_{x}v_{x0}+v_{x0}^2}{a_{x}^2})\) \(x=x_{0}+\frac{v_{x0}v_{x}}{a_{x}}-\frac{v_{x0}^2}{a_{x}}+\frac{1}{2}(\frac{v_{x}^2}{a_{x}}-\frac{2v_{x}v_{x0}}{a_{x}}+\frac{v_{x0}^2}{a_{x}})\) \(x-x_{0}=\frac{v_{x0}v_{x}}{a_{x}}-\frac{v_{x0}^2}{a_{x}}+\frac{1}{2}(\frac{v_{x}^2}{a_{x}})-\frac{v_{x}v_{x0}}{a_{x}}+\frac{1}{2}(\frac{v_{x0}^2}{a_{x}})\) \(x-x_{0}=\frac{1}{2}(\frac{v_{x}^2}{a_{x}}-\frac{v_{x0}^2}{a_{x}})\) \(2a_{x}(x-x_{0})=v_{x}^2 -v_{x0}^2\) \(v_{x}^2=v_{x0}^2+2a_{x}(x-x_{0})\) These equations can be used for any given direction, not just in the x-direction; however, position, velocity and acceleration must be occurring in the same direction for this equation to make sense: i.e. \(v_y=v_{y0}+a_{y}t\) [amp-cta id="9459"] A cannonball is shot out of a cannon and its velocity relative to the \(\textbf{x}\)-axis is given by the equation \(\textbf{v = 20 – 10t}\). At what time \(\textbf{t}\) will the cannonball come to a rest momentarily (neglecting the force of friction)? The first question we ask ourselves is, what variable helps determine when an object is at rest? Velocity! When \(v\) is equal to \(0\), we know that any object is not moving at time \(t\), regardless of its acceleration. Therefore: \(v=20-10t\) \(0=20-10t\) \(20=10t\) \(t=2\). This means at \(2\) seconds, the cannonball will have come to a rest momentarily. Why do we say momentarily? This is because the cannonball still has acceleration: We are given that the baseline velocity equation is: \(v=v_0 +at\) Using the equation, \(v=20-10t\), we know that at time \(t=2\), \(v=0\). Also, at time \(t=0\), \(v_0 =20-10(0)=20\). This means that at time \(t=2\), \(a=\frac{v-v_0}{t}=\frac{0-20}{2}=-10 m/s^2\). A nonzero acceleration just implies that at some point, the cannon ball changes direction. After \(2\) seconds, the cannonball will change directions and move in the opposite direction of initial movement. A ball rolls off a table that is \(\textbf{4.9}\) meters tall. The ball at the edge of the table has a velocity of \(\textbf{8 m/s}\). At what distance \(\textbf{x}\) from the edge of the table will the ball land? First, we have to realize that the velocity of the ball at the edge of the table only impacts the \(x\) direction. So what is the velocity in the \(\textit{y}\) direction? That’s an equation we have to determine ourselves! We know that relative to the ground, the initial position is \(4.9 m\), initial velocity in the \(y\) direction is \(0 m/s\) and that acceleration is a result of gravity (\(-9.8 m/s\)). Therefore, our position equation in the \(y\) direction is given as: \(y=y_0 + v_{y0}+\frac{1}{2}at^2\) \(y=4.9-\frac{1}{2}9.8t^2\) Our next step is to find how long the ball takes to reach the ground. We can do so by setting \(y\) to \(0 m\) to find that \(t\) is: \(0=4.9-\frac{1}{2}9.8t^2\) \(4.9t^2 =4.9\) \(t^2 =1\) \(t=1\) Now that we know how long the ball takes to reach the floor, all we have to do is figure out the distance the ball ends up from the edge of the table! We know that the velocity of the ball in the \(x\) direction at the edge of the table is given by \(v_x = 8 m/s\). This velocity is both the initial velocity at the edge of the table and is constant, since we don’t have any acceleration in the horizontal direction (there are no horizontal forces acting on the ball). Therefore, we can use the following equation to determine the distance the ball lands away from the table: \(x=x_0 + v_{x0}t+\frac{1}{2}at^2\) \(x=0+(8)t+\frac{1}{2}(0)t^2\) \(x=8t\) Since we know the ball lands on the ground at time \(t=1\), we get: \(x=8(1)\) \(x=8 m\). Therefore, the ball lands \(8\) meters away from the table! We know that kinematics covers situations in which acceleration is constant. But how do we find acceleration? In addition to acceleration being the rate of change of velocity over time as shown above, it is also equal to the net force exerted on the system divided by the mass: It is important to note that acceleration in the \(x\) direction, \(y\) direction or \(z\) direction is proportional to the total net force in the \(x\) direction, \(y\) direction or \(z\) direction, respectively. We mentioned earlier that kinematics may also relate to uniform circular motion. This acceleration, known as centripetal acceleration, points towards the center of rotation and is perpendicular to the velocity of the object. Centripetal acceleration is equal to the velocity squared divided by the radius of the circle. A car drives around a circular track with a radius of \(\textbf{10 m}\). The tangential velocity of the car at any given point is \(\textbf{20 m/s}\). What is the acceleration? We know that \(a_c =\frac{v^2}{r}\), therefore the centripetal acceleration is given as: \(a_c =\frac{20^2}{10}\) \(a_c =40m/s^2\) The same concepts applied under the Acceleration, Velocity and Position section can be applied for rotational motion. Angular position (\(\theta\)) is analogous to position just as angular velocity (\(\omega\)) and angular acceleration (\(\alpha\)) are analogous to velocity and acceleration, respectively. The corresponding angular motion kinematics equations used on the AP Physics 1 exam are shown below. Just like linear position, velocity and acceleration, angular velocity is the rate of change in angular position over time while angular acceleration is the rate of change in angular velocity over time. A bug is stuck to the edge of the tire of a car. The bug travels \(\textbf{5m}\) to complete one rotation. If the angular velocity of the bug is given at \(\textbf{4 m/s}\), how many rotations does the bug make in \(\textbf{20}\) seconds? The first thing to note is that the bug has \(0\) angular acceleration since the angular velocity is constant and not dependent on time. This means that the equation for angular position is given as: \(\theta=0+4t+0\) \(\theta=4(20)\) \(\theta=80m\) If the angular distance traveled is \(80m\) and one rotation is completed in \(5m\), that means the bug made \(80/5=16\) rotations on the tire. We hope you’ve gained a stronger grasp of the kinematics equations on the AP Physics 1 exam! You don’t need to memorize these equations since they will be provided to you. Rather, it is important to understand when these equations are applicable and how they might help you analyze a situation. As you take more practice exams and review for the AP exam, you will get better at quickly identifying which formulas will help you get the answer the test is looking for. For more practice, see the official College Board example questions and our ultimate guide to the AP Physics 1 exam. What’s Covered:
How Will AP Scores Impact My College Chances?
Overview of AP Physics 1 Exam
Exam Layout

Scoring
Kinematics Equations You Need to Know + Practice Problems
Acceleration, Velocity, and Position
![]()
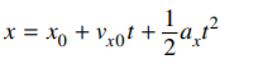
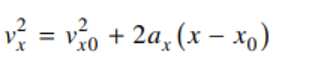

Practice Problem: Determining Acceleration
Practice Problem: Ball Rolling Off a Table
Acceleration: A Deeper Understanding
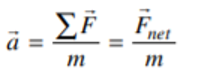
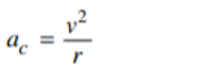
Practice Problem: Determining Centripetal Acceleration
Angular Acceleration, Velocity and Position
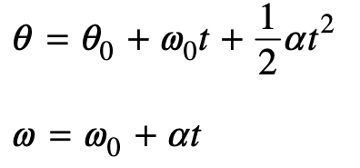
Practice Problem:
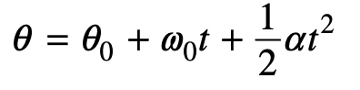
Wrapping It Up