IB Math SL Exam Practice Questions
What’s Covered:
- Overview of the IB Math SL Exam
- IB Math SL Exam Questions
- Calculator Suggestions for IB Math SL
- Final Tips
- How Does the IB Math SL Exam Affect My College Chances?
The following blog post is about the International Baccalaureate Diploma Programme (IB / IBDP), and its associated examinations. Please refer to CollegeVine’s ultimate guide to IB for more information!
Overview of the IB Math SL Exam
The IB Math SL examination consists of two individual papers, each designed to test the student on different applications of the coursework taught during the two-year course. The two papers are formatted as such:
- Paper 1 – 90 marks / 90 minutes long / No calculator permitted
- Paper 2 – 90 marks / 90 minutes long
The two exams cover most of the coursework for the class, but since paper 1 is not to be taken with a calculator, you’ll find the formatting and styling of the questions in this paper to differ from paper 2. This is because the questions are designed such that a calculator wouldn’t be of much use anyway in solving them. Since the two tests have different styling, the kind of student you are with your strengths and weaknesses determine which exam you’ll excel in.
IB Math SL Exam Questions
The best way to prepare for both papers is to collect previous examinations, or past papers. Then, solve as many past papers as you can while referring to the rubric of each paper respectively. The IB rubric or mark scheme tells you how to solve problems in the most efficient way possible, which is usually the way in which IB will give working marks for. To start, let’s look at some example problems and solutions for paper 1.
These questions are taken from official previous specimen papers from the IBO. These are publicly available and can also usually be found at your school.
Paper 1 – Question 1
Solution:
a. Median Weight = Middle position = 210 g
b. Upper Quartile = middle of section covering median to the heaviest puppy = 240 g
c. Interquartile Range = Upper quartile (Q3) – Lower Quartile (Q1) = Q3 – Q1 = 240 – 190 = 50g
d. Heaviest puppy that is not an outlier = Q3 +1.5(Interquartile Range)
It’s recommended to use 1.5 here because according to the markscheme and coursework, this is the best coefficient to test for how much of an outlier a data point is.
Because we’re trying to test for a heavy puppy, a value that will be high, we add instead of subtract here. If we the outlier was a lighter puppy, then we’d subtract.
Q3 +1.5(Interquartile Range) = 240 + 1.5(50) = 315 g
Paper 1 – Question 2
Solution:
a. Whole numbers involved = Discrete data
b. Mean number of classes = 2
\(2=\frac{(0*20)+(1*24)+(2*30)+(3*k)+(4*10)+(5*3)+(6*1)}{20+24+30+k+10+3+1}\)
\(2=\frac{145 + 3k}{88 + k}\)
\(176+2k = 145 + 3k\)
\(k=31\)
c. The specific kind of sampling technique used in this is systematic sampling. This is a sampling technique where members of the data set or population are selected at regular intervals.
That wraps the sample questions for paper 1. However, an exam would have more than just three questions, so make sure to thoroughly practice past papers, to not only answer more questions correctly but to also better manage the stress of a time limit.
You’ll find that paper 2 presents longer/lengthier problems, and might have overall less questions. This is because each question has multiple subsections, and arriving at a final answer requires proper execution in these subsections. So for example if you find the first subsection (a) of a question difficult, you could struggle with the next part because it builds off the answer in (a). Instead, drop this question momentarily and try another one, then come back to it later! Now, here are some problems and solutions for paper 2!
Paper 2 – Question 1
Solution:
a. Perimeter at an area of 25 = \(4\sqrt{25}\) or \(4(5)=20\)
b. Range of \(P(A)= 0 \lt P(A) \lt n\)
Domain of \(A= 0 \lt A \lt 25\)
The largest possible value for \(P(A)\) exists in largest value in domain, which is 25.
Therefore, \(n = 20\).
c. The inverse function is always the reflection of the original.
The green line on the graph below indicates the axis in which it reflects against.
The red line is the inverse function.
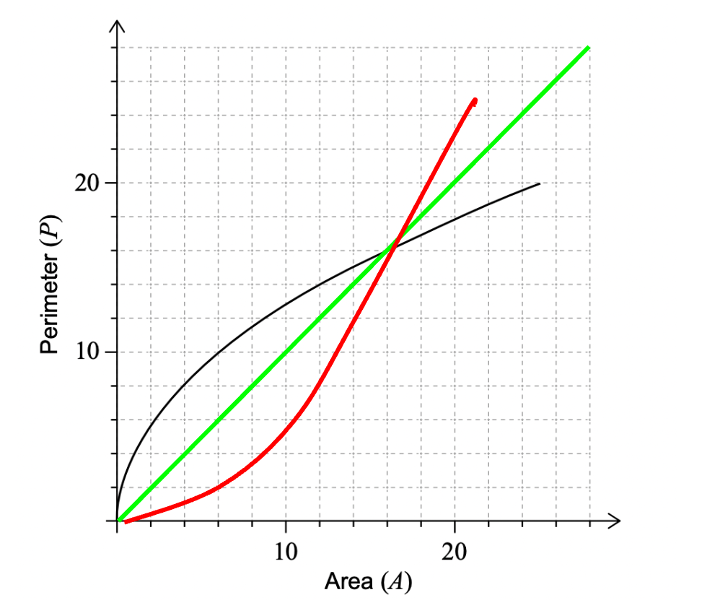
d. \(P^{-1}(18)=4\) implies that when the perimeter is 8, the area of the square is 4.
Paper 2 – Question 2
Solution:
a (i). Number of payments (\(N\)) = 24 (6 years, 4 times a year)
Interest (\(I\)) % = 14%
Principal Value (\(PV\)) = 14,000 (-14,000 in the case that money is being spent)
Number of payments (\(PY\)) = 4
Compounding periods per year (\(CY\)) = 4
If you’re using an IBO certified calculator, which you should be for this exam as any other calculator would result in disqualification of the exam, then input these values into the financial app section of your calculator. This option is available in any IBO permitted calculator and is encouraged to make this process of the exam more efficient.
Payments each quarter = 871.82
a (ii). Total amount paid = \(871.82 \cdot 24 = 20923.68\)
a (iii). Interest paid = Total amount paid – \(PV = 20923.68-14000=6923.68\)
b (i). Amount borrowed with option B \(= 14000 – (14000 \cdot 10\) % deposit)
\(= 14000-14000(0.1) = 12600\)
b (ii). This question will require you to use the TVM function in the finances app on your permitted calculator only. Input the amount borrowed, the deposit and number of years for the answer.
r = 12.56%
c. Interest paid in option A \(= 6923.68\)
Interest paid in option B \(= (250 \cdot 72)-12600 = 5400\)
The interest in option B is significantly lower, hence Bryan should go with option B.
d. We need to use the following formula to solve this question:
\(FV = PV \cdot (1+\frac{r}{100k})^{kn}\)
Where \(FV\) is the future value, \(PV\) is the present value, \(r\) is the nominal annual interest rate, \(k\) is the number of compounding periods per year, and \(n\) is the number of years.
The value of our variables is as follows:
\(PV = 14000\)
\(r = 25%\)
\(n=6\)
\(k = 1\)
Now using the formula mentioned earlier, we do the following:
\(FV = 14000 \cdot (1-\frac{25}{100})^6 = 2491.70\)
This concludes our practice problems and solutions! If you managed to make it through and you feel confident in your approach to these problems, perfect! These problems are on the harder end of the exams, especially that last one. Now let’s cover what tools are permitted for the examination.
Calculator Suggestions for IB Math SL
There are certain kinds of calculators allowed for paper 2 of the examinations, so make sure to adhere to these rules. Failure to do so will be shown during the mandatory calculator check done by the host/invigilator of the exam, with penalties being as severe as disqualification.
While there are numerous “accepted” calculators, not all of them are great. The following list contains the most used, and best graphic/scientific calculators for IB Math SL (and HL too!)
- Ti84 plus (all models)
- Ti Nspire (non-CAS models) with the 84 faceplate
- Ti83 plus
- Casio CFX 9850 Plus
- Casio FX 9950 Plus
Keep in mind, they all perform the same functions. It’s just that they’re more efficient, quicker on the operations, and have much more user-friendly interfaces. Make sure to, regardless of whatever calculator you choose to use, put it in exam mode.
Final Tips
Exams are hard, but here are some quick and easy tips to make it more manageable for you!
Practice Lots of Papers
There’s no better way to prepare for an exam than doing practice papers. Studying practice papers not only helps you learn how to solve math problems, and IBO does tend to repeat lots of questions annually (with just slight differences in numbers/wording). If you’re lucky, you might come across a question in an exam that seems familiar from practice!
Don’t Stay Up Late
Staying up late the night before an exam is one of the most common exam-prepping mistakes students make! Studying at such hours in a tired state would likely not be productive, and would only leave you feeling drowsy and tired during the exam the following day. Instead, go to bed early, and if you need to revise or practice a little extra before your exam, wake up early!
How Does the IB Math SL Exam Affect My College Chances?
The exam itself doesn’t really affect your chances, but the class itself shows colleges that you’re taking challenging classes. It’s important to show initiative and motivation in your applications, which is exactly what IB courses are known for given their difficulty. Instead of stressfully wondering how your chances into a university stack up, try CollegeVine’s free admissions calculator! This tool uses a multitude of inputs from standardized test scores and GPA to extracurriculars, to predict your shot at getting into your dream school!