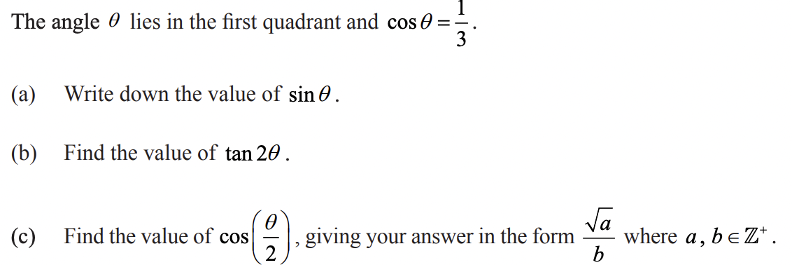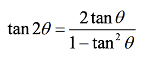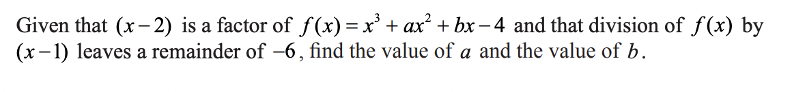IB Math HL Exam Practice Questions
What’s Covered:
- Overview of the IB Math HL Exam
- IB Math HL Practice Exam Questions
- Calculator Suggestions for IB Math HL
- Final Tips
- How Does the IB Math HL Exam Affect My College Chances?
The following post is about the International Baccalaureate Diploma Program, also called IBDP for short, and its examinations. The program entails the selection of numerous rigorous courses, including mathematics. IB Math HL is full of extensive coursework and difficult exams, but this guide is going to help you break down the exams into manageable information, which will help you succeed!
For more info about IB, check out CollegeVine’s ultimate guide to IB for more information.
Overview of the IB Math HL Exam
The IB Math HL exam consists of three different tests, each referred to as a paper. The three papers are formatted slightly differently from each other and differ on calculator requirements. These three papers are formatted as such:
- Paper 1: 100 marks / 2 hours long / No calculator
- Paper 2: 100 marks / 2 hours long / Calculator allowed
- Paper 3: 50 marks / 1 hour long / Calculator allowed
All three exams cover the same set of coursework in different styles, but since paper 1 isn’t calculator permitted, you’ll find that the formatting of the questions differ. This is done intentionally, with the purpose to present questions that don’t require long calculations but rather unorthodox mindsets to solve.
IB Math HL Practice Exam Questions
There’s no better way to practice for IB examinations than to go through previous past papers or specimen papers. Specimen papers are sets of exams that IBO releases to teachers and students, to give an idea of what the upcoming examination set might be like. These are valuable resources to get yourself accustomed to not only the content of the exams, but also the formatting of them too!
These questions are taken from specimen papers from the IBO.
Paper 1 – Question 1
Solution:
(a) Since it’s given that angle \(\theta\) lies in the first quadrant, we know that \(\sin{\theta}\) , \(\cos{\theta}\) , and \(\tan{\theta}\) are all positive values. Let’s use the following given formula to determine \(\sin{\theta}\).
Then, \((\frac{1}{3})^2 + \sin ^2 \theta =1\).
\(\sin^2 \theta = \frac{8}{9}\)
\(\sin{\theta} = \frac{\sqrt{8}}{3}\)
(b) We can use the following formula to compute \(\tan{2\theta}\):
To find \(\tan{\theta}\) , we can use the previous result: \(\tan{\theta}= \frac{\sin{\theta}}{\cos{\theta}} = \sqrt{8}\).
So, \(\tan{2\theta}= \frac{2\sqrt{8}}{1 – 8} = -\frac{2\sqrt{8}}{7}\).
(c) To find the value of \(\cos{\frac{\theta}{2}}\), we’ll need a variation of the following formula:
From this formula, we get that: \(\cos{\frac{\theta}{2}} = \sqrt{\frac{1}{2}(\cos{\theta} + 1)}\).
All we need to do is plug in the appropriate values to solve for \(\cos{\frac{\theta}{2}}\):
\(\cos{\frac{\theta}{2}}=\sqrt{\frac{1}{2}(\frac{1}{3}+1)}=\sqrt{\frac{2}{3}}=\frac{\sqrt{6}}{3}\)
Paper 1 – Question 2
Solution:
(a) Let’s start by calculating the probability that no heads are obtained from \(n\) coins being tossed. Keep in mind that the probability of obtaining no heads is the same as the probability of obtaining all tails.
First, let’s determine the probability that no head is obtained from one coin being tossed. There is an equal chance of getting a head or a tale, so the probability is 50%, or \(\frac{1}{2}\).
Because each coin toss is independent, the probability of coin one AND coin 2 both not being a head would just be \(\frac{1}{2} \cdot \frac{1}{2}\). (We are able to just multiply the probability for each because the events are independent.)
So, the probability that no heads are obtained from \(n\) coins being tossed is:
\(P(no\ heads\ from\ n\ coins\ being\ tossed)=\frac{1}{2} ^n\)
Now let’s find the probability that no head is obtained relative to the balls selected.
If ball 1 is selected: \(P(no\ head)=\frac{1}{2} ^1 = \frac{1}{2}\)
If ball 2 is selected: \(P(no\ head)=\frac{1}{2} ^2 = \frac{1}{4}\)
If ball 3 is selected: \(P(no\ head)=\frac{1}{2} ^3 = \frac{1}{8}\)
The probability that each ball is selected is just \(\frac{1}{3}\), since there is an equal amount of chance of selecting each ball.
Because the ball selection and coin toss are independent events, to find the probability of selecting a ball AND obtaining no heads can be found by multiplying the probability of each event.
So, we have the following formula, where we multiply the chance of getting each ball (\(\frac{1}{3}\)) by the chance of obtaining no heads for each ball. We then sum the results to get our answer.
\(P(no\ head) = P(no\ heads\ from\ ball\ 1)\ or\ P(no\ heads\ from\ ball\ 2)\ or\ P(no\ heads\ from\ ball\ 3)\)
\(P(no\ head)= (\frac{1}{3} \cdot \frac{1}{2}) + (\frac{1}{3} \cdot \frac{1}{4}) + (\frac{1}{3} \cdot \frac{1}{8}) = \frac{7}{24}\)
(b) To find the probability of event \(A\) given event \(B\), we have the following formula:
\(P(A|B) = \frac{P(A \bigcap B)}{P(B)}\)
So, the probability of 2 coins tossed given no heads is as follows:
\(P(2\ coins\ tossed\ given\ no\ heads)=\frac{P(2\ coins\ and\ no\ head)}{P(no\ head)}=\frac{\frac{1}{3}\cdot \frac{1}{2} ^2}{\frac{7}{24}}=\frac{2}{7}\)
The probability of getting no heads is \(\frac{1}{2}\), raised to the number of times tossed, which is 2 here. This is multiplied by \(\frac{1}{3}\) because that is the probability of pulling a ball with a certain desired number on it. We found the probability of no heads in the previous part of this problem.
That wraps up the question and solutions for paper 1. You’ll notice that the questions aren’t too lengthy but do require some understanding of concepts and functions, because a calculator isn’t permitted. Paper 2 will usually have harder questions, so even though a calculator is permitted, it doesn’t necessarily mean the exam could be easier! Moving on, here are some questions from paper 2!
Paper 2 – Question 1
Solution: \(a=1, b=-4\)
If \((x-2)\) is a factor of \(f(x)\), this means that \(f(2)=0\). Similarly, if dividing by \((x-1)\) leaves a remainder of \(-6\), then \(f(1)=-6\).
We can use these facts to solve for \(a\) and \(b\) by plugging in \(2\) and \(1\) into \(f(x)\):
\(f(2) = (2)^3 + a(2)^2 + b(2) – 4 = 4a + 2b +4\)
\(f(1) = (1)^3 + a(1)^2 + b(1) – 4 = a+b-3\)
Knowing that \(f(2)=0\) and \(f(1)=-6\) gives:
\(4a+2b+4=0\)
\(a+b-3=-6\)
We can simplify to get the following system of equations:
\(4a+2b=-4\)
\(a+b=-3\)
Solving the second equation for \(a\) gives: \(a=-b-3\).
Now, we can plug this into the first equation to get:
\(4(-b-3)+2b=-4\)
\(-4b-12+2b=-4\)
\(-2b=8\)
\(b=-4\)
Then, we have that \(a=-(-4)-3=1\).
If you have extra time, you’d probably want to plug these values back into \(f(x)\) to double check that they’re correct.
Paper 2 – Question 2
Solution: \(a=16, r=\frac{3}{4}\)
We have that the first term of a geometric series is \(a\), and the common ratio is \(r\). This means that each term of the series is equivalent to the previous term multiplied by \(r\). So, the series would look as such:
\(a, a(r), a(r)^2, a(r)^3, …\)
Then, we have that the third term is \(a(r)^2\).
Next, the sum of a geometric series is given by the following formula:
\(\frac{a}{1-r}\)
Since we are given the values for the third term and the sum of the series, we have the following two equations:
\(a(r)^2 = 9\)
\(\frac{a}{1-r}=64\)
We can simplify the second equation:
\(a=64(1-r)\)
We can now plug this into the first equation:
\(64(1-r)(r^2)=9\)
\(64r^2 – 64r^3 – 9=0\)
Using a calculator, we get that \(r=\frac{3}{4}\). Then, \(a=16\).
Calculator Suggestions for IB Math HL
The following calculators are not only permitted to be used for exams by IBO, but also make taking exams much easier! They have functions and applications that make tedious and hard calculations much easier, saving time for the harder bits of the exam. Here are some recommendations:
- Ti84 plus (all models)
- Ti Nspire (non-CAS models) with the 84 faceplate
- Ti83 plus
- Casio CFX 9850 Plus
- Casio FX 9950 Plus
These calculators all perform the same functions similarly, so it comes down to personal preference after trying them out.
Final Tips
Practice Questions Without a Calculator
Even though paper 2 and 3 allow the use of a calculator in the exam, try practicing as many questions from past exams without the calculator. This not only makes you better at performing mental math, but also more time-efficient with the exams. If you’re able to perform the calculations mentally, you could spend less time using a calculator for questions that could actually be solved quicker in your head! This reserves excess time for questions that could be harder. That being said, if you find yourself consistently making errors via mental math, please be sure to check your work with a calculator.
Practice SL Questions
Find yourself struggling with HL past examinations and questions? You might be lacking a proper foundation or understanding of basics to perform the harder tasks expected in HL coursework. To tackle this small problem, just try SL past examinations. SL papers test students on basics and the grounding foundations of mathematics and concepts that make up HL. This is why SL papers are valuable resources even for HL students!
How Does the IB Math HL Exam Affect My College Chances?
The exam itself doesn’t really affect your chances, but the class itself shows colleges that you’re taking difficult classes with the intention of trying your hardest. This level of determination is important in college applications, along with many other factors! You might need a better understanding of what your chances of admission into a university look like, and it’s easily done with CollegeVine’s admissions calculator. This intuitive tool uses a multitude of inputs such as GPA, extracurriculars and standardized test scores to determine your chances of admission to a university of your choosing!