31 ACT Math Formulas You Need to Know
In theory, the ACT Math Test seems fairly straightforward: 60 questions in 60 minutes, calculator permitted. Every question is multiple-choice, and there’s also no guessing penalty, which means that wrong answers won’t deduct any points from your total score. For more information on scoring specifics, check out the Complete Guide to Your ACT Score Report. Topics covered on ACT Math include middle and high school algebra, plane and coordinate geometry, statistics and probability, and trigonometry. Unlike on the SAT, however, the ACT doesn’t provide a formula sheet/box for reference during the test. As such, it’s crucial that you memorize the formulas you’ll need and practice using them ahead of test day. In this post, we’ll discuss why the ACT matters and which formulas are important for success on ACT Math. Your GPA and standardized test scores are used to calculate your academic index, which determines whether you pass the first stage of the admissions process at most colleges. This is because colleges want students who will thrive academically and graduate on time, so they prefer applicants who have a demonstrated history of solid academic performance. Altogether, high school transcripts and test scores provide some projection of your likely future success in the classroom, and the academic index becomes an efficient method for screening out academically unqualified students. As such, think of your ACT score as a prerequisite. It determines whether you’ll pass the academic cutoff and make it into the next stage, which is holistic review: essays, extracurriculars, and letters of recommendation. Excellent ACT scores can further qualify you for scholarships, honors programs, and other special opportunities. This is why the ACT is important, but it generally won’t be the deciding factor in your acceptance. To better understand how ACT scores can affect your chances, check out our free Admissions Calculator! Unlike other chancing engines, it also considers your high school coursework, extracurriculars, goals, and achievements in building your college list and assisting with your applications. Now that we’ve established why the ACT matters, let’s discuss the math formulas you need to know. \(a_n=a_1+(n-1)d\) This formula defines a sequence of numbers where the difference between each consecutive term is the same. The first term of the sequence is \(a_1\), the \(n^{th}\) term of the sequence is \(a_n\), and the constant difference between consecutive terms is \(d\). This formula defines a sequence of numbers where given the first term, each successive term is defined by multiplying the previous term by a fixed number, also known as the common ratio \((r)\). As with arithmetic sequences, the first term of the sequence is \(a_1\), and the \(n^{th}\) term of the sequence is \(a_n\). \(log_b(b^x)=x\) Logarithms are the inverse functions of exponents. In other words, the logarithm of a number, \(x\), is the exponent to which another number, the logarithmic base \(b\), must be raised to produce \(x\). You’ll likely need to rewrite logarithms on the ACT using the following formulas: If \(log_b(x)=y\), then \(b^y=x\). \(log_b(xy)=log_b(x)+log_b(y)\) \(log_b(\frac{x}{y})=log_b(x)-log_b(y)\) \(d=rt\) This is a common algebraic relationship where \(d\) is distance, \(r\) is rate, and \(t\) is time. You can rewrite this equation to isolate \(r\) or \(t\), and “distance” can be replaced with the more general concept of “quantity.” Just be sure to keep your units straight! \(f\:\circ\:g(x) =f(g(x))\) This is a composite function, where the output of \(g(x)\) is the input for \(f(x)\). Notice that \(f\:\circ\:g(x)\) is different from \(fg(x) = f(x)\:\times\:g(x)\). \(\pi\:radians = 180^{\circ}\) This is a useful conversion to memorize for trigonometry problems, especially those involving the coordinate plane. To boost your speed, make sure to have the unit circle memorized! \(\frac{y_2-y_1}{x_2-x_1}=m\) Slope is a rate, specifically \(\frac{rise}{run}\). The slope of any line, \(m\), can be determined given any two points on the line, \((x_1,y_1)\) and \((x_2,y_2)\). \(y=mx+b\) This equation defines a line with slope \(m\) and a y-intercept of \((b,0)\) that passes through the point \((x,y)\). \(\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=d\) This formula calculates the distance, \(d\), between two points \((x_1,y_1)\) and \((x_2,y_2)\). \((\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\) This formula defines the midpoint of the line between two points, \((x_1,y_1)\) and \((x_2,y_2)\). \((a+b)(c+d) =ac+ad+bc+bd\) We use FOIL to multiply 2 binomials together. Below are some FOIL shortcuts to memorize, where \(y\) is a constant: \((x+y)(x+y)=(x+y)^2=x^2+2xy+y^2\) \((x-y)(x-y)=(x-y)^2=x^2-2xy+y^2\) \((x+y)(x-y)=x^2-y^2\) If \(ax^2+bx+c=0\), then \(x=\frac{-b\:\pm\:\sqrt{b^2-4ac}}{2a}\) The quadratic formula provides values of \(x\), also known as solutions/roots/zeros, for a given quadratic function \(ax^2+bx+c=0\), where \(a\), \(b\), and \(c\) are constants. The expression underneath the square root, \(b^2-4ac\), is called the discriminant and determines the number of solutions. Specifically: \(y=a(x-h)^2+k\) This formula defines a quadratic function with the vertex at \((h,k)\) and a constant, \(a\), determining stretch and direction. The axis of symmetry is line \(x=h\), which crosses the vertex. Note that FOIL will convert this equation to an expanded form. As such, you may be asked to factor back into vertex form in order to provide coordinates for the vertex. \((x-h)^2+(y-k)^2=r^2\) This equation defines a circle with center point \((h,k)\) and radius \(r\). As with the quadratic function above, FOIL will convert this equation to an expanded form, and you may be asked to factor in order to find the radius or central coordinates. Angles along a line are called supplementary angles, adding up to \(180^{\circ}\). Complementary angles add up to \(90^{\circ}\), a right angle. Vertical angles describe angles directly across from one another, which are always congruent. In the diagram to the left, for example, we would say that angles 1 & 2 are supplementary, while angles 1 & 3 are vertical angles. \(\frac{1}{2}bh=A\) This equation provides the area \((A)\) of any triangle given lengths of the base \((b)\) and height \((h)\). Note that height is the length of the line extending at a complementary angle from any side (the base) up to the point/angle directly across from that side. For equilateral triangles, where all three sides \((s)\) are the same length, the area equation is: \(\frac{s^2\sqrt{3}}{4}=A\) Image courtesy of SAT As angles in a triangle always add up to \(180^{\circ}\), a right triangle is defined as any triangle with one right angle, ensuring the other two angles are complementary. The side lengths of right triangles can be defined by the Pythagorean Theorem: \(a^2+b^2=c^2\) Here, \(a\) and \(b\) are the lengths of the legs, or the sides across from the complementary angles, and \(c\) is the length of the hypotenuse, the side across from the right angle. It may be helpful to also memorize the following Pythagorean triples, or values for side lengths \((a,b,c)\): 3-4-5, 5-12-13, 7-24-25, and 8-15-17. Note that the hypotenuse is always the longest side. There are two types of special right triangles, which have the angles and length ratios as follows: Image courtesy of SAT \(A = lw\) This formula provides the area of a rectangle with length \(l\) and width \(w\). \(A = bh\) This formula provides the area of a parallelogram given base \(b\) , the length of the longest sides, and height \(h\), defined as the length of the line extending at a complementary angle up from one base to the other. \(A=\frac{b_1+b_2}{2}\:\times\:h\) This formula provides the area of a trapezoid with bases \(b_1\) and \(b_2\) and height \(h\), defined the same way as for parallelograms. \((n-2)\:\times\:180^{\circ}= S\) In a regular polygon, where all sides and angles are equal, this formula provides the sum \((S)\) of the interior angles given a polygon with \(n\) sides and angles. We can also find each interior angle by calculating \(\frac{S}{n}\). \(\frac{\theta}{360^{\circ}}\:\times\:2\pi r=arc\:length\) This formula defines the length of the arc, or section of the circle circumference, between two given radii intersecting at the circle center with central angle \(\theta\). Note that the \(2\pi r\) incorporates circle circumference into this formula. \(\frac{\theta}{360^{\circ}}\:\times\:\pi r^2 = sector\:area\) Similar to arc length, this formula provides the area of the sector between two given radii intersecting at the circle center with central angle . The \(\pi r^2\) incorporates circle area into this formula. \(SA = 2(lw + wh + lh)\) \(V= lwh\) These formulas provide the surface area \((SA)\) and volume \((V)\) for a rectangular prism with length \(l\), width \(w\), and height \(h\). \(V=\pi r^2h\) This is the volume formula for a right cylinder with base radius \(r\) and height \(h\). Should you need the surface area or volume formulas for any other 3D shapes, the ACT will provide relevant formulas in the questions themselves. Most ACT trig problems involve manipulating sine, cosine, and tangent, which are calculated as follows for given angle \(x\) in a right triangle: \(sin(x)=\frac{opposite\:leg}{hypotenuse}\) \(cos(x)=\frac{adjacent\:leg}{hypotenuse}\) \(tan(x)=\frac{opposite\:leg}{adjacent\:leg}=\frac{sin(x)}{cos(x)}\) SOH-CAH-TOA is an easy mnemonic for remembering which trig function corresponds to which side lengths! \(sin(x) = cos(90^{\circ}-x)\) \(cos(x) = sin(90^{\circ}-x)\) In words, these identities show that a trig function of angle \(x\) equals the value of the cofunction of the complement of \(x\). They are generally used when dealing with more advanced trigonometry, allowing for easy conversions between sine and cosine. You may occasionally see the reciprocal identities of \(sin(x)\), \(cos(x)\), and \(tan(x)\), which are: \(csc(x) =\frac{1}{sin(x)}\) \(sec(x) =\frac{1}{cos(x)}\) \(cot(x) =\frac{1}{tan(x)}\) \(sin^2(x)+cos^2(x)=1\) Based on the Pythagorean Theorem and the unit circle, this identity is generally used alongside the cofunction identities to solve trig problems (sans calculator) where angle \(x\) or the values of these trig functions of \(x\) are unknown. \(n\% \:of\:m = \frac{n}{100}\:\times\:m\) Percentages are used to express parts of a whole, and the \(\%\) symbol generally means “divide by 100.” As such, the above equation answers any problem asking for \(n\%\) of quantity \(m\). The ACT tests basic statistical knowledge, generally involving the measures below: \(P(A) = \frac{number\:of\:desired\:outcomes}{total\:number\:of\:possible\:outcomes}\) Probability represents the likelihood of an event \((A)\) occurring, calculated by dividing the number of desired outcomes by the number of total possible outcomes. For instance, the probability of rolling a 6 on an even-sided dice is \(\frac{1}{6}\). \(P(A\:and\:B) = P(A)\:\times\:P(B)\) Events \(A\) and \(B\) are independent if \(A\) occurring does not affect the probability of \(B\) occurring. To calculate the probability that both independent events will occur, we multiply their individual probabilities together. For instance, the probability of flipping heads twice is \(\frac{1}{2}\:\times\:\frac{1}{2}=\frac{1}{4}\). We’ve covered lots of formulas in this post, but be sure to also review all math concepts through Algebra II and Geometry! For instance, you can expect complex numbers, vectors, matrices, systems of equations, and manipulating graphical functions to be on the test as well. See this full description of the ACT math section for more info. Remember that practice makes perfect, especially for math! You’ll want to try lots of different problems before test day, with the goal of really understanding how to apply and integrate these concepts and formulas in a timely manner. As you are allowed a calculator for the ACT, we would advise bringing one, but with a word of caution. Remember that every ACT math problem can be solved without a calculator, and it’s easy to waste valuable time by using your calculator when you actually don’t need to. As such, do timed practice sections with your calculator if you plan to bring one, and remember that it’s only there as a last resort: to ease calculations and increase your speed. Reach for it rarely, and check that your specific model is permitted per the ACT calculator policy. For more tips on ACT Math, check out these blog posts: What’s Covered:
How Do ACT Scores Impact Your College Chances?
Numbers and Quantities
1. Arithmetic Sequences
2. Geometric Sequences
3. Logarithms
4. Rates
5. Function Notation
6. Radians to Degrees
Graphs and Coordinate Geometry
7. Slope of a Line
8. Slope-Intercept Formula
9. Distance Formula
10. Midpoint Formula
11. FOIL (First, Outer, Inner, Last)
12. Quadratic Formula
13. Vertex Form
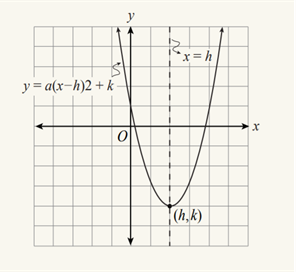
Image courtesy of ACT14. Graphing Circles
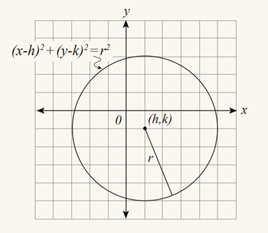
Image courtesy of ACT
Plane Geometry
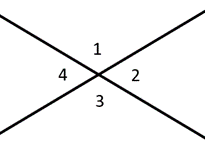
15. Angles and Lines
16. Area of a Triangle
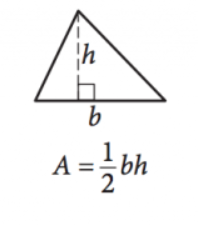
Image courtesy of SAT17. Pythagorean Theorem
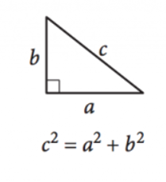
18. Special Right Triangles
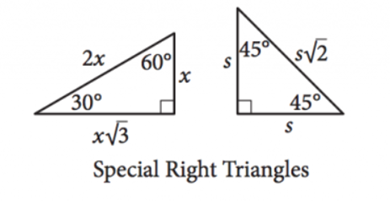
19. Areas of Quadrilaterals
20. Interior Angles of Regular Polygons
21. Arc Length in a Circle
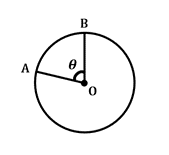
22. Sector Area in a Circle
23. 3D Shapes
Trigonometry
24. SOH-CAH-TOA
25. Cofunction Identities
26. Ratio/Reciprocal Trig Identities
27. Pythagorean Identity
Statistics and Probability
28. Percentages
29. Mean, Median, Mode, and Range
30. Probability
31. Independent Events
Wrapping It Up