SAT Math Prep: Lines and Slopes
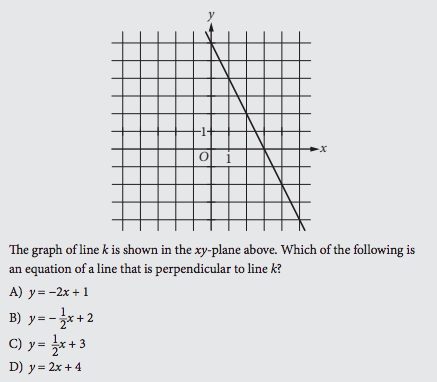
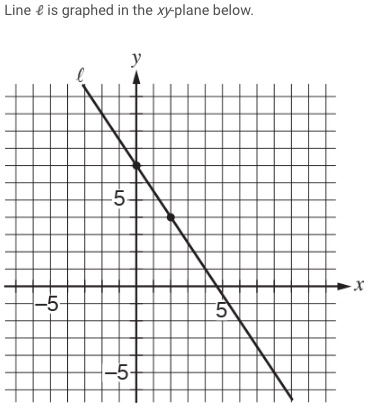
The SAT Math section can be challenging for many students. Fortunately, knowing what types of problems you’ll need to tackle and equations you’ll need to memorize is half the battle. Lines and slopes are important concepts for the Heart of Algebra section of your math SAT. How can you prepare for this type of problem? Keep reading to learn all about lines and slopes, equations you should know, and examples (with explanations) to help you practice. A line is a one-dimensional figure that is completely straight with no curvature and no thickness. Made up of connected dots, it extends infinitely in both directions. A slope, otherwise known as a gradient, is the measure of the steepness or slant of a line. It is the ratio of the rise (the change in distance vertically over the \(y\)-axis) to the run (the change in distance along the \(x\)-axis). Before you attempt to tackle problems or memorize equations involving lines and slopes on your SAT, it’s important to understand some fundamental properties of these concepts. The basics include: Formulas are provided on the SAT, but it will save you time to memorize important ones beforehand. That way, you can tackle the problems without having to flip back to check the formulas. The equation of a line (also known as slope-intercept form): \(y=mx+b\) \(m\) is the slope and \(b\) is the \(y\)-intercept. It’s a good idea to rewrite any line equation into the form above to simplify solving any questions. To find the slope: \(\frac{y_2-y_1}{x_2-x_1}\) Example #1 (Source: College Board’s Study Guide: Heart of Algebra) In the above problem, line \(k\) passes through points \((0,6)\) and \((3,0)\). Remember the formula for finding the slope of a line: \(\frac{y_2-y_1}{x_2-x_1}\) So in this case, the equation is \(\frac{6-0}{0-3}\) The result is \(-2\). Remember that the slopes of perpendicular lines have a product of \(-1\), or must be negative reciprocals of each other. Therefore, the line perpendicular to line \(k\) must have a slope of \(\frac{1}{2}\). In slope-intercept form, the coefficient of x is the slope of the line. So the correct answer is C, the equation with a slope of \(\frac{1}{2}: y=\frac{1}{2}x + 3\). Example #2 (Source: Official SAT Study Guide: Sample Math Questions) If line ℓ is translated up \(5\) units and right \(7\) units, then what is the slope of the new line? A) \(\frac{2}{5}\) B) \(\frac{−3}{2}\) C) \(\frac{−8}{9}\) D) \(\frac{−11}{14}\) Remember your original formula: \(\frac{y_2-y_1}{x_2-x_1}\) The key to answering this problem quickly and correctly is to remember that translating the line (moving the line somewhere else) will not change the slope of the line. Moving the line up \(5\) units and over \(7\) only changes the coordinates of line ℓ, but not the slope. So, using the original points on the graph as indicators, \((2,4)\) and \((0,7)\), the slope of line ℓ would be: \(\frac{4-7}{2-0}\) In this case, the slope is \(\frac{-3}{2}\), so the correct answer is B) \(\frac{-3}{2}\). For more practice questions to study up for the SAT, check out the 15 Hardest SAT Math Questions. Looking for help acing your SAT? Download our free guide with our top 8 tips for mastering the SAT.

What are Lines and Slopes?
What Line and Slope Properties Should You Know?
Lines and Slopes Formulas to Know
This represents the change in \(y\)-values divided by the change in \(x\)-values. \((x_1, y_1)\) is a coordinate pair from the line, and \((x_2, y_2)\) is another coordinate pair from the same line.Examples of Lines and Slopes SAT Problems
Wrapping it Up