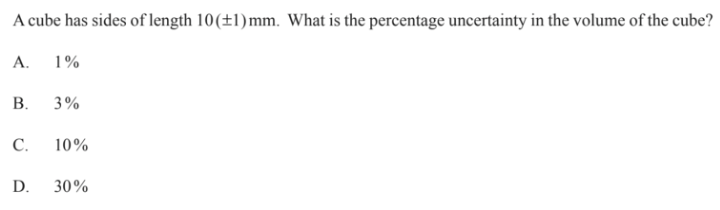IB Physics SL Exam Practice Questions
What’s Covered:
- Overview of the IB Physics SL Exam
- IB Physics SL Exam Questions
- Calculator Suggestions for IB Physics SL
- Final Tips
- How Does the IB Physics SL Exam Affect My College Chances?
The IB Physics SL Exam is a fairly difficult examination. It’s important to practice as much as possible in order to pass the exam. The following blog post will cover some practice questions, along with detailed explanations for how to solve them. Please refer to CollegeVine’s Ultimate Guide to IB for more information about the IB program!
Overview of the IB Physics SL Exam
The IB Physics SL exam has three papers, and the three exams are structured and formatted differently in order to test the student on different aspects of the coursework. The exams are formatted as such:
- Paper 1 (MCQ) – 30 marks / 45 minutes long / No calculator permitted
- Paper 2 – 50 marks / 75 minutes long / Calculator permitted
- Paper 3 – 35 marks / 60 minutes long / Calculator permitted
These exams cover a majority of the coursework in physics SL. You will find that the formatting/styling of the questions in paper 1 differs from the others given that it contains multiple choice questions (MCQ). All three papers are different in their questions, so which paper you excel at is determined by how much you’ve practiced for the specific kind of paper and what kind of student you are.
IB Physics SL Exam Questions
There’s no better way to prepare for examinations than to practice past papers and solve questions. The repetition of building knowledge of concepts and familiarizing yourself with the formatting of the paper will help you excel in the subject fast. It’s especially useful to do this along with a rubric for each past paper you study! The rubric (also called a mark scheme) tells you the right answer for questions in an exam, and the work required to get there (with full working marks!). Let’s begin with a couple questions and solutions for the MCQ, paper 1.
These questions are taken from official previous specimen papers from the IBO. These questions are not from official previous exams. These are usually given at your school, so you may be able to request your teacher for a copy.
Paper 1 – Question 1
Answer: D
Let \(A\) represent the side length, and let \(dA\) represent the uncertainty in the side length of the cube. Then, \(\frac{dA}{A}\) represents the percentage uncertainty in the side length of the cube.
Next, let \(V\) represent the volume of the cube, and let \(dV\) represent the uncertainty in the volume of the cube. Then, \(\frac{dV}{V}\) represents the percentage uncertainty in the volume of the cube, which is what we’re trying to find.
Knowing the formula for the volume of a cube gives us the following equation:
\(V=A^3\)
Because the volume is the cube of the side length, the percentage uncertainty in the volume will be three times the percentage uncertainty of the side length.
So, \(\frac{dV}{V}=3\frac{dA}{A}\)
From the problem, we know that \(A=10\) and \(dA=1\). Let’s plug that into our equation:
\(\frac{dV}{V}=\frac{3(1)}{10}=0.3=30\)%
Therefore, option D is correct
Paper 1 – Question 2
Answer: C
From the formula sheet, you’re given the following two equations, where \(x\) represents the displacement and \(v\) represents the velocity:
\(x=x_{0}\sin{\omega\ t}\)
\(v=\omega\ x_{0}\cos{\omega\ t}\)
Given that velocity is the derivative of displacement, it makes sense that velocity follows a cosine graph when displacement follows a sine graph.
The question mentions that velocity leads the displacement by a phase angle \(\phi\). We should already know that the cosine graph is equivalent to the sine graph, but shifted over by \(\frac{\pi}{2}\).
So, the phase angle is \(\frac{\pi}{2}\), and the correct answer is C.
Paper 1 – Question 3
Answer: B
Knowing the properties of sound waves is important for the IB Physics exam. So, this question should rely on memorization only.
Sound waves fit category one, refraction, and category three, diffraction. They do not fit category two, polarization. So, only options one and three are valid, and the correct option is B.
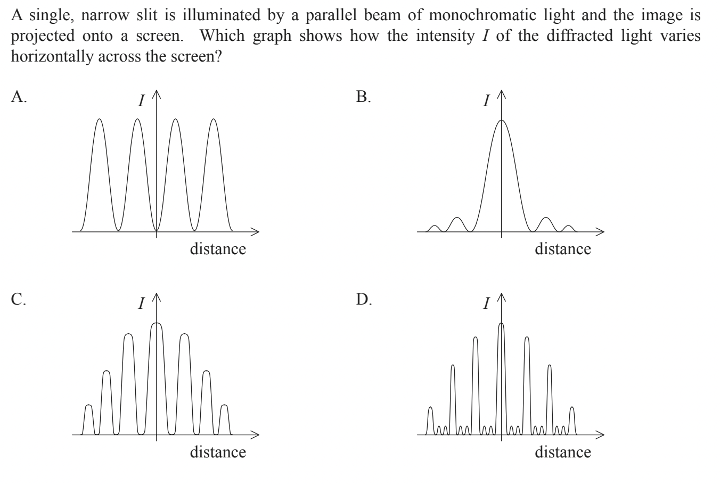
Paper 1 – Question 4
Answer: B
The width of the central maxima, which can be used to measure intensity (I), is dependent on the size of the slit and the distance from the screen.
Graph B best represents the effects of distance from the screen on the intensity of the light on the screen. When the distance is zero, the intensity should be at the maximum. So, option A is incorrect. As the distance increases, the intensity decreases significantly. Option B best captures this trend.
You’ll notice paper 1 questions aren’t particularly difficult, but the paper overall might be hard due to the time constraint of completing numerous questions in such a short time. Moving on, here are some paper 2 questions and solutions!
Paper 2 – Question 1(a)
Answer: \(t=9.8\ s\)
Let’s use this kinematic equation, since we know the initial speed:
\(v=v_0 +at\), where \(v\) is the final velocity, \(v_0\) is the initial velocity (on the way down), \(a\) is the acceleration, and \(t\) is time.
We are told that the initial velocity is \(48 m/s\). The final velocity will be the velocity at which the container hits the bottom of the vacuum. Because air resistance is negligible, the final velocity will have the same magnitude as the initial velocity. However, since the final velocity points in the opposite direction (downwards), we know that it’s \(-48 m/s\). The acceleration here is the value of gravitational acceleration, which according to the provided data booklet, is \(-9.81 m/s^2\).
Now, we can plug these values into our equation.
\(-48=48-9.81t\)
So, \(t=9.8\ s\)
Paper 2 – Question 1(b)
Answer: \(F=6.9\cdot 10^4\ N\)
Here we use another kinematic equation that is provided in the data booklet.
\(v^2 =v_0 ^2 -2a\Delta x\)
This equation uses the same variables as the last one, but this time we have \(\Delta x\) which is the distance of the object moved instead of time, \(t\).
The initial velocity is \(-48\ m/s\), because we stated in part (a) that the container hits the bottom of the tank at \(48\ m/s\). The final velocity is \(0\ m/s\), since the container will come to a stop. \(\Delta x\) is \(8.0\ m\), since that’s the distance it takes for the container to stop moving. We can plug all these values in to solve for acceleration (which we’ll need to calculate force):
\(0^2 =48^2 -2a(8)\)
\(a=144\ m/s^2\)
Remember, for this paper a calculator is permitted, so make sure to take advantage of that!
Now that we know our acceleration value, we can find force, knowing that:
\(F=ma\), where \(F\) is force, \(m\) is mass (which we’re told is \(480\ kg\)), and \(a\) is acceleration.
\(F=480\cdot 144=6.9\cdot 10^4 \ N\)
Paper 2 – Question 1(c)
Answer:
The experiment inside the container can be considered weightless because the reaction force is \(0\), and because both the object and container will fall at the same rate!
Paper 2 – Question 2(a, i)
Answer: \(1.97\cdot 10^9 \ \frac{J}{s}\)
The energy provided by the natural gas each second is the same as the power. We have the following formula for power:
\(power = \frac{power\ output\cdot 100}{efficiency}\)
\(power =\frac{7.5\cdot 10^8 \cdot 100}{38}=1.97\cdot 10^9 \ \frac{J}{s}\)
Paper 2 – Question 2(a, ii)
Answer: \(56\ \frac{MJ}{kg}\)
Here we divide the calculated power from part (i), by the rate at which the natural gas burns:
\(\frac{1.97\cdot 10^9}{35}=56\ \frac{MJ}{kg}\)
Paper 2 – Question 2(b)
Answer:
Most of the world’s energy is from fossil fuels simply because of its abundance as a resource and its ease of acquisition, which is mining.
Paper 2 – Question 2(c, i)
Answer:
The following are reasons for why the temperature may increase:
- Increased amounts of greenhouse gasses in the atmosphere
- More absorption of infrared in the atmosphere
- Increase in energy radiated back to the ground
Paper 2 – Question 2(c, ii)
Answer:
Scientists try to tackle the debate regarding the validity of climate change by providing improved modeling for data, making it easier for the masses to understand information and facts. They also might strive for more internal collaboration.
Hopefully, these examples have given you a better idea of what to expect out of paper 2. Now let’s try some paper 3 problems!
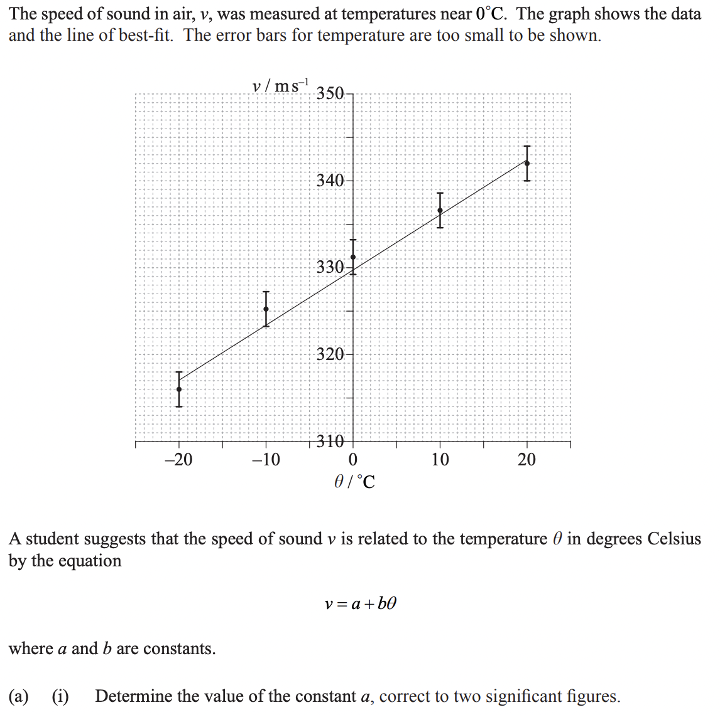
Paper 3 – Question 1 (a, i)
Please note that this guide will not cover option specific questions, just general ones!
Answer: \(a=330\ m/s\)
\(a\) is just the point at which the line intersects the axis. In this case, if we read the graph carefully, we can see that \(a=330\ m/s\).
Paper 3 – Question 1(a, ii)
Answer: 0.08
The calculations for uncertainty are as follows:
\(b_{max} =\frac{upper\ bound\ of\ maximum\ coordinate\ (y-axis)-upper\ bound\ of\ minimum\ coordinate\ (y-axis)}{range\ of\ temperature\ (x-axis)}\)
\(b_{min} =\frac{lower\ bound\ of\ maximum\ coordinate\ (y-axis)-lower\ bound\ of\ minimum\ coordinate\ (y-axis)}{range\ of\ temperature\ (x-axis)}\)
The upper and lower bounds of each point are marked above, with the upper bounds being red, and the lower bounds blue.
\(b_{max}=\frac{344-316}{40}=0.70\)
\(b_{min}=\frac{340-318}{40}=0.55\)
Then, \(b=\frac{b_{max}-b_{min}}{2}=\frac{0.70-0.55}{2}=0.075\).
Rounding up, we get \(b=0.08\)
Paper 3 – Question 2(a)
Answer: 1.2%
The estimated percentage of uncertainty can be found by multiplying the coefficient of the derivative for t (2) by the percentage uncertainty for measurement of time, then adding it to the coefficient of the derivative for h (1) multiplied by the percentage uncertainty for the measurement of height:
\(2(0.3)+1(0.6)=1.2\)%
Paper 3 – Question 2(b)
Answer:
The student could get a more reliable measurement for g by using a smaller ball, which reduces air resistance. They could also use a larger height and repeat the process more often to get a more reliable result.
Calculator Suggestions for IB Physics SL
While there are a bunch of accepted models for IB Physics HL and SL, some are better than others! The following calculators are IBO permitted and have functions and tools that make them easy to use. Just make sure to double check the most recent list of accepted calculators at your school too!
- Ti84 plus (all models)
- Ti Nspire (non-CAS models) with the 84 faceplate
- Ti83 plus
- Casio CFX 9850 Plus
- Casio FX 9950 Plus
All these calculators perform the same functions, but try them out and see which one is easier for you to use and perform best with. And most importantly, make sure the calculator of your choosing is in “exam mode,” protecting you from any sort of cheating-related suspicions.
Final Tips
IB exams are hard, and physics is no exception. In fact, you could argue that physics is one of the harder science subjects offered in IB, but excelling in it doesn’t have to be impossible! Try these small tips and you’ll see a great boost in your academic performance and mental well-being when things get stressful!
Spend Extra Time in the Lab
Paper 3 requires extensive knowledge of technical and methodological applications of the knowledge taught during the course. The only way to perfect this understanding and practice, is to spend more time in a lab performing more experiments. This will accustom you to the “realistic” scenarios of IB physics, and make Paper 3 seem much easier!
Time Yourself While Practicing
Practicing older exams and papers is already an amazing way of preparing for the exams, but making sure to place yourself on a realistic time limit and recreate the conditions of an actual exam as much as possible will make it even better. The time limit might seem like extra pressure but, nailing these papers with the time limit will be useful for when the actual exams roll around! By this point, your time-management during the paper will be spot-on!
How Does the IB Physics SL Exam Affect My College Chances?
In short, it doesn’t! Your actual exam scores don’t make much of an impact on your college admissions, but showing determination to take harder classes does! The initiative and motivation speak more than the actual test scores. If this seems confusing or you need further clarity on what does matter for college admissions, check out CollegeVine’s admissions calculator, which takes GPA, extracurriculars, standardized test scores and much more into consideration to tell you your shot of getting into your dream schools!